Protecciones de escollera en un tramo de rambla
Planteamiento del problema
Una rambla se encuentra encauzada en zona urbana mediante muros y tiene una sección transversal rectangular de 100 m de ancho. El caudal empleado para el diseño del encauzamiento fue de 2500 m3/s.
El primer kilómetro de encauzamiento presenta un trazado recto en planta en dirección este-oeste. Los primeros 500 m tienen una pendiente longitudinal del 0,5% y los 500 m siguientes una pendiente longitudinal del 1%.
Seguidamente el encauzamiento presenta una curva girando 90º hacia el sur, con un radio de curvatura de 500 m. A la salida de la curva, el encauzamiento vuelve a presentar una alineación recta en dirección norte-sur en una longitud de 500 m. Tanto en la curva como en el tramo final la pendiente longitudinal continua siendo del 1%.
Tras una avenida reciente se han producido erosiones aguas arriba de la curva, en la propia curva e inmediatamente aguas abajo de la misma. Se plantea proteger con escollera el lecho del tramo de rambla que ha sufrido erosión, dimensionando dicha protección.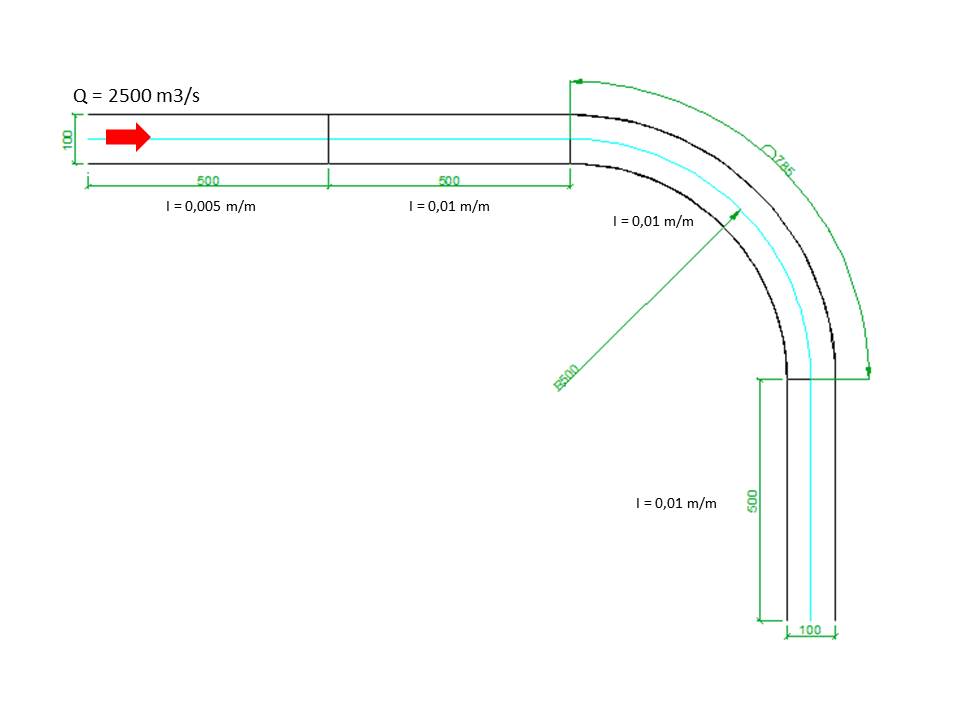
Figura 1. Planta con la definición geométrica del encauzamiento de la rambla
Protección del tramo recto aguas arriba de la curva (pendiente 1%)
La fórmula propuesta de Maynord et al. (1987) es aplicable para el diseño de protecciones generales, es decir, no locales (que no están sometidas a fuertes turbulencias) y para cauces rectos, en el fondo y en taludes hasta 1V:2H. Cuando existen caídas, obstáculos, etc. es necesario recurrir a otra formulación.
La fórmula permite realizar una estimación del diámetro característico de la escollera con el objeto de que no sufra arrastre. La fórmula es válida para elementos con continuidad longitudinal y del lado de la seguridad para protecciones continuas o mantos continuos. Contempla el mecanismo de fallo por arrastre de la escollera por el flujo. Dicha fórmula tiene la siguiente expresión general:
Siendo:
D30 = diámetro de la escollera para el que el 30% de la muestra (en peso) es inferior (m)
y = calado medio en la sección sobre la escollera (m)
γ = peso específico del agua (kN/m3)
γs = peso específico de la escollera (kN/m3)
v = velocidad media en la sección sobre la escollera (m/s)
g = aceleración de la gravedad (9,81 m/s2)
El coeficiente de valor 1,2 se corresponde con el factor de seguridad del diseño y el coeficiente de valor 0,3 se corresponde con la condición de inicio de movimiento de las partículas.
La metodología se complementa con recomendaciones relativas al coeficiente de Manning de la escollera y a la granulometría, es decir:
Siendo:
D90 = diámetro de la escollera para el que el 90% de la muestra (en peso) es inferior (m)
n = coeficiente de rugosidad de Manning.
En cuanto al espesor, para garantizar el correcto funcionamiento de la protección, se recomienda de 2*D30 ó 1,5*D50, con una distribución granulométrica con varianza σ2 = 1,7 – 5,2.
Normalmente, es necesario disponer de un filtro adecuado bajo la escollera que evite problemas en el substrato por fuga de finos, que originen el fallo de la protección.
Como resulta que las magnitudes hidráulicas (calado y velocidad) dependen del tamaño de la escollera y viceversa, el procedimiento de resolución es iterativo.
Partimos de un valor inicial para el D30, por ejemplo 0,3 m.
El valor del D90 sería:
El valor del coeficiente de rugosidad de Manning:
Y el valor del calado se obtiene a partir de la fórmula de Manning:
Siendo:
Q = caudal (m3/s)
A = sección mojada (m2)
Rh = radio hidráulico (m)
Io = pendiente longitudinal (m/m)
Resolviendo la ecuación anterior se obtiene un valor del calado y = 3,981 m.
La velocidad sería:
Y el número de Froude:
Y aplicando la fórmula de Maynord se obtiene el valor de D30 para la escollera:
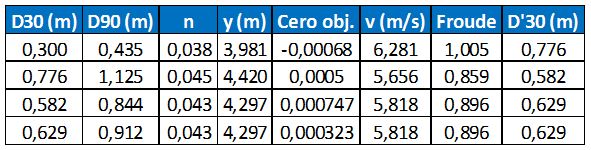
Partiendo del valor obtenido de 0,776 m para el D30 se continúa con el cálculo de forma iterativa, hasta que el valor de partida coincide con el valor resultante, tal y como se muestra en la tabla siguiente:
Tabla 1. Proceso iterativo para el cálculo del D30 de la escollera
Por lo tanto, el valor del D30 resulta ser de 0,629 m.
Para obtener el peso característico “P” asociado al tamaño de escollera D30 se puede aproximar la forma de la escollera a un elipsoide, cuyos ejes deben cumplir la condición:
Siendo:
(a + b)/(2*c) = índice de planaridad,
a = eje mayor del elipsoide,
b y c = ejes menores, siendo c < b, y por lo tanto “b” es la dimensión del elemento de escollera que determina el paso por el tamiz.
Esta condición pretende evitar la presencia de elementos planos en la escollera.
Si b = 0,629 m, entonces a = (3/2)*b = 0,944 m y c = (5/8)*b = 0,394 m, cumpliendo que el índice de planaridad no supera el valor de 2.
El volumen del elipsoide sería:
Y el peso característico del tamaño D30 sería:
A continuación se define un huso granulométrico comprendido entre una curva granulométrica mínima y una curva granulométrica máxima y se propone una curva granulométrica comprendida en dicho huso para la escollera en cuestión, tal y como se observa en la tabla siguiente:
Tabla 2. Huso granulométrico definido por una curva mínima y una curva máxima. Curva granulométrica propuesta para la escollera de protección del lecho del cauce
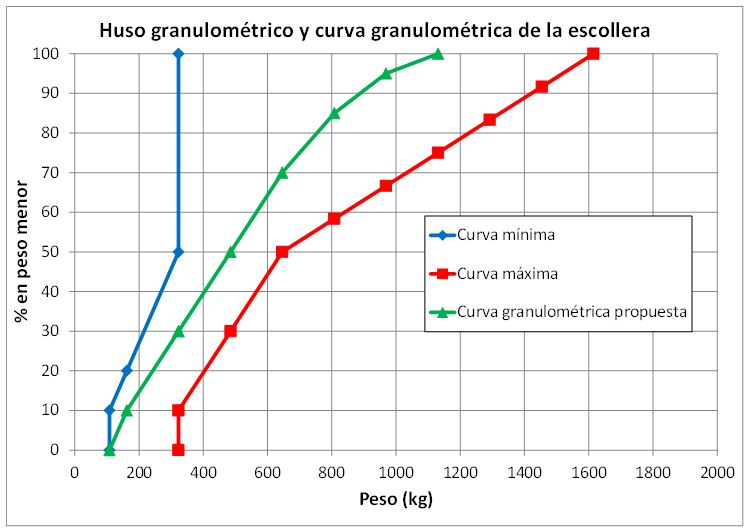
Y en forma de gráfico, la curva granulométrica propuesta sería:
Gráfico 1. Huso granulométrico y curva granulométrica de la escollera de protección
La escollera propuesta para proteger el lecho del tramo recto de la rambla en cuestión tendría la siguiente curva granulométrica:
Tabla 3. Curva granulométrica propuesta para la escollera de protección del lecho del cauce
En cuanto al espesor, para garantizar el correcto funcionamiento de la protección, se recomienda de 2*D30 = 2*0,629 = 1,258 m ó 1,5*D50 = 1,5*0,720 = 1,080 m. Por lo tanto, se podría colocar un espesor mínimo de escollera de 1,25 m.
La distribución granulométrica debe tener una varianza σ2 comprendida entre 1,7 y 5,2. En este caso, el valor de la varianza sería σ2 = 1,711 que está entre 1,7 y 5,2.
Protección de la curva de radio 500 m
Es de interés el estudio de la curva dada a la rambla en el encauzamiento. En la sección transversal tiene lugar una corriente secundaria a la que se le atribuye la responsabilidad de modelar la sección transversal de la curva del encauzamiento, y que explica que el lado exterior sea más hondo por efecto del descenso de la corriente secundaria.
La sobreelevación del nivel de agua entre la orilla exterior e interior, por causa de la fuerza centrífuga, se puede obtener mediante la siguiente expresión:
Siendo:
Δy = la sobreelevación en la curva (m)
v = la velocidad media (m/s)
B = el ancho del cauce (m)
r = el radio de curvatura (m)
En nuestro caso, el valor de la sobreelevación es:
Por lo tanto, el calado puede llegar a alcanzar un valor de 4,297 + 0,690 = 4,987 m
Asumiendo el valor del número de Froude de 0,896 obtenido en el apartado anterior:
Si b = 0,727 m, entonces a = (3/2)*b = 1,092 m y c = (5/8)*b = 0,456 m, cumpliendo que el índice de planaridad no supera el valor de 2.
El volumen del elipsoide sería:
Y el peso característico del tamaño D30 sería:
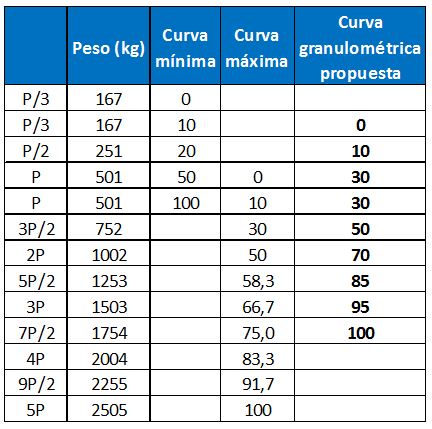
A continuación se define un huso granulométrico comprendido entre una curva granulométrica mínima y una curva granulométrica máxima y se propone una curva granulométrica comprendida en dicho huso para la escollera en cuestión, tal y como se observa en la tabla siguiente:
Tabla 4. Huso granulométrico definido por una curva mínima y una curva máxima. Curva granulométrica propuesta para la escollera de protección del lecho del cauce en la curva
Y en forma de gráfico, la curva granulométrica propuesta sería:
Gráfico 2. Huso granulométrico y curva granulométrica de la escollera de protección en la curva del encauzamiento
La escollera propuesta para proteger el lecho del tramo en curva de la rambla en cuestión tendría la siguiente curva granulométrica:
Tabla 5. Curva granulométrica propuesta para la escollera de protección del lecho del cauce en la curva del encauzamiento
En cuanto al espesor, para garantizar el correcto funcionamiento de la protección, se recomienda de 2*D30 = 2*0,727 = 1,454 m ó 1,5*D50 = 1,5*0,833 = 1,250 m. Por lo tanto, se podría colocar un espesor mínimo de escollera de 1,50 m.
La distribución granulométrica debe tener una varianza σ2 comprendida entre 1,7 y 5,2. En este caso, el valor de la varianza sería σ2 = 2,299 que está entre 1,7 y 5,2.
Aguas abajo de la curva se protegería con la misma escollera que aguas arriba de la curva.
Figura 2. Planta con la definición geométrica del encauzamiento de la rambla y con la protección de la escollera en el lecho
Bibliografía
1) López Alonso, R. 2004. Problemas resueltos de ingeniería hidráulica forestal. Departamento de Ingeniería Agroforestal. Universitat de Lleida.
2) Martín Vide, J.P. 2009. Ingeniería de ríos. Edicions UPC.


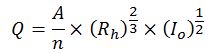
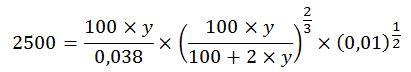
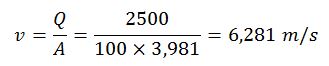
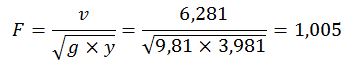
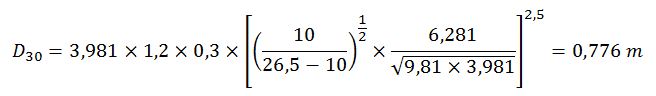
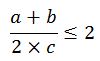
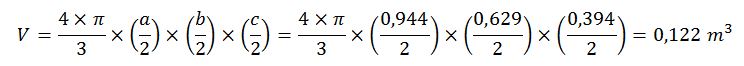


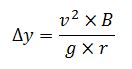
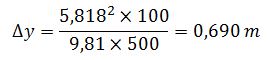
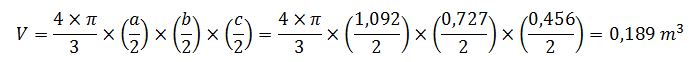



10 Comments
Roberto Curiel says: 2018/02/26 at 20:59 //
Muy interesante el artículo, estoy desarrollando un proyecto en el que necesitaba calcular este tipo de escollera. La duda que tengo es como calcular tamaño para el resto de los pesos, si lo pudieras publicar te lo agradecería mucho.
rauhermi says: 2018/02/27 at 10:13 //
Buenos días Roberto, una vez que tienes los pesos puedes obtener los volúmenes dividiendo por el peso específico de la escollera. Y una vez que tienes los volúmenes puedes aplicar la fórmula del volumen del elipsoide, dejándolo todo en función del eje “b”, haciendo uso de las siguientes fórmulas:
V=(4*pi/3)*(a/2)*(b/2)*(c/2)
a=(3/2)*b
c=(5/8)*b
Cumpliendo de esta manera con la condición de planaridad ((a + b)/(2*c)<=2) Recuerda que "b" es la dimensión del elemento de escollera que determina el paso por el tamiz. Saludos. Raúl.
rauhermi says: 2018/02/28 at 11:25 //
D85/D15 o D84/D16 es un parámetro adimensional que se emplea como medida de dispersión y que se suele llamar varianza granulométrica. Se recomienda que la varianza granulométrica se encuentre entre 1,7 y 5,2.
David Lopez says: 2018/07/04 at 09:01 //
Hola Raúl, compañero de estudios y murciano como yo.
Muy buen artículo para entender y adoptar correctamente los valores de la formulación de Maynord et al.
Una pregunta, ¿en que momento se deben tener en cuenta valores de CsubT y CsubA distintos a la unidad, de la ecuación general?
Muchas gracias.
rauhermi says: 2018/07/05 at 09:45 //
Hola David, me alegro de saludarte y gracias por contactar a través del blog de Es el agua.
En relación a tu consulta de la fórmula de Maynord, CT es el coeficiente de espesor de capa en función de la relación de uniformidad d85/d15 y se recomienda adoptar el valor CT=1. Mientras que CV es el coeficiente de distribución de la velocidad y se recomienda:
– CV=1.0 para canales rectos o interior de curvas.
– CV=1.283 – 0.2 log (Rc/W) en zona exterior de curvas. Siendo Rc el radio de curvatura de la curva (m) y W el ancho de la lámina de agua aguas arriba de la curva (m)
– CV=1.25 aguas abajo de canales de hormigón y final de canales y espigones.
Saludos.
Raúl.
David says: 2018/07/05 at 10:09 //
Muchas gracias por tu respuesta.
He formulado un problema de encauzamiento trapezoidal de unos 10 m de ancho ( 5,70 en base) con un caudal de unos 30 m3/seg y una pendiente longitudinal del 2% y obtengo con Maynord un d30 de 0.25m tras realizar la iteraciones. ¿No crees que es una escollera muy pequeña esta? Apenas son 35 kg de peso.
Gracias de nuevo Raúl. Enhorabuena por el blog
rauhermi says: 2018/07/05 at 11:23 //
Hola de nuevo David. Con esas dimensiones que comentas y admitiendo un coeficiente de rugosidad de Manning de 0,045 debes de tener un calado de alrededor de 1,2 m, una velocidad media próxima a 3 m/s y un número de Froude en torno a la unidad. Con estos valores de las magnitudes hidráulicas, quizás en lugar de proponer un manto de escollera continuo y una pendiente longitudinal uniforme te puedes plantear otras alternativas. Por ejemplo, puedes corregir la pendiente longitudinal haciendo un escalonamiento del lecho (reduciendo la pendiente), mediante vigas riostras transversales y colocando bandas de escollera inmediatamente aguas abajo de cada caída. De esta forma ahorrarías mucha escollera, ya que colocarías una escollera más grande en franjas de cierta anchura (p.e. de 5 m,…) de forma discreta cada cierta distancia (p.e. cada 200 m,…).
Saludos.
Raúl.
Cristian says: 2019/05/15 at 23:54 //
Estimado,
Muy interesante el tema, le quería preguntar si tiene algún estudio empírico realizado en enrocados (tamaño de rocas superior a 75mm) y como influye la permeabilidad en estos tipos de suelo. Y de acuerdo a esto como va influyendo el tamaño de poros, el espacio de vacío y la velocidad del agua.
Quedo atento a tu respuesta,
Saludos,
Cristian Aguilar
Figaro says: 2020/07/11 at 11:27 //
Hola,,,no entiendo que significa y que indica en la gráfica “% en peso menor”….¿podrías aclarar este concepto??….gracias
Edwin Alexander López Vásquez says: 2020/11/05 at 21:22 //
Buenas tardes, saludos desde Perú; tengo una duda sobre socavación en curvas, ya que he hallado las formulas pero no logro entenderlas al 100% como para plasmarlas en un plano, tendrá alguna referencia sobre ello.