Impulsiones. Diámetro económico. Punto de funcionamiento. Golpe de ariete. Protecciones
Elevación desde el río Segura hasta el Canal Principal de la Margen Derecha (Azud de Ojós)
1. INTRODUCCIÓN
Continuando con la reciente categoría inaugurada en el blog de www.eselagua.com “flujo en presión” se presenta un nuevo post en el que se realiza un estudio completo de una impulsión, desde la elección del diámetro económico de la tubería, la determinación del punto óptimo de funcionamiento (H, Q) y la elección de la bomba más adecuada, el análisis del golpe de ariete que se produce debido a una interrupción súbita en el suministro eléctrico, la influencia de la inercia de las masas rotantes del grupo de bombeo en la variación del caudal y en las envolventes de presiones máximas y mínimas, y por último la disposición de un calderín, a la salida del bombeo, como protección antiariete.
Se considera la impulsión con una válvula de retención instalada a la salida del grupo de bombeo, y en la que no se produce la separación de la columna líquida, por cavitación, durante el transitorio.
2. PLANTEAMIENTO DEL PROBLEMA
Se plantea elevar un caudal de 5,5 m3/s desde un río, a la cota de toma de 147 m, hasta un canal cuya solera arranca a la cota 300 m. Tras el correspondiente estudio topográfico y geológico-geotécnico del terreno se elige un trazado con una longitud de impulsión de 427 m.
Tras consultar a diferentes fabricantes de tuberías se decide ejecutar el tramo de impulsión con tubería de fundición dúctil, siendo la rugosidad absoluta de la misma 0,03 mm y el módulo de Young de 166.770 MPa.
El régimen de funcionamiento de la impulsión es de doce de la madrugada a 8:00 h de la mañana de lunes a viernes y durante las 24 h los fines de semana, lo que supone un número de horas de funcionamiento anual de 4.576 h.
Tras las oportunas gestiones se ha logrado una tarifa eléctrica a contratar de 0,0978 €/kwh.
3. ELECCIÓN DEL DIÁMETRO ECONÓMICO
Se sabe que un menor diámetro supone un menor coste de ejecución, pero mayores costes de explotación, debidos a las mayores pérdidas por fricción, que redundan en un mayor coste energético. El diámetro económico será aquel con el que la suma de ambos costes sea mínima.
Haciendo uso de la fórmula que proporciona el diámetro económico aproximado, propuesta por el profesor emérito de la Universidad de Córdoba D. José Agüera Soriano, que se basa en la fórmula de Vibert, y que tiene en cuenta el coste de la tubería a instalar, el coste del equipo de bombeo y el coste de la energía eléctrica que hay que pagar durante la vida útil de la instalación: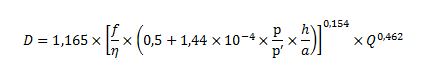
Siendo:
D: diámetro en metros, f: coeficiente de fricción, η: rendimiento de la bomba, p: precio del kwh, p’: precio de referencia del kwh, h: número anual de horas de funcionamiento, a: factor de amortización, Q: caudal en m3/s.
El factor de amortización se calcula mediante la fórmula: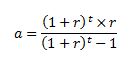 
Siendo:
r: el interés real (interés nominal menos el valor de la inflación), t: años de vida útil de la instalación.
Para una tasa de interés real del 4% y una vida útil de 50 años, a = 0,047.
Admitiendo un valor inicial del coeficiente de fricción de 0,015, un rendimiento de la bomba de 0,7 y un precio de referencia de 0,0741 €/kwh, los demás datos de la fórmula son conocidos, por lo tanto:
El diámetro comercial interior más próximo para la tubería de fundición dúctil seleccionada es 2,221 m.
Obsérvese que en la obtención del diámetro económico no ha intervenido la altura geométrica, ni tampoco la longitud de la impulsión. Sin embargo, el número de horas de funcionamiento del bombeo es fundamental en el cálculo del mencionado diámetro.
4. ELECCIÓN DE LA BOMBA. PUNTO DE FUNCIONAMIENTO
Para el cálculo de la pérdida de carga por rozamiento en la tubería se hace uso de la fórmula de Darcy–Weisbach: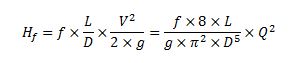
Las nuevas variables que aparecen en esta fórmula son la longitud de la tubería “L” en m, la velocidad “V” en m/s y el caudal “Q” en m3/s. La aceleración de la gravedad se representa con la letra “g” y su valor es de 9,81 m/s2. El diámetro se sigue representando por “D” en metros. Y el coeficiente de fricción “f”, admitiendo régimen turbulento intermedio, depende de la rugosidad relativa y del número de Reynolds, y se puede obtener a partir de la fórmula de Colebrook:
Siendo:
Re: el número de Reynolds,
εr: la rugosidad relativa.
El número de Reynolds de calcula como:
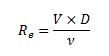Siendo “ν” la viscosidad cinemática del fluido en m2/s.
La velocidad media del flujo es:
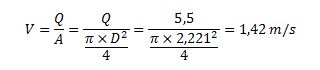Para un valor de viscosidad cinemática de 1,003.10-6 m2/s, el número de Reynolds es:
Que confirma la existencia de un régimen turbulento.
La rugosidad relativa sería:
Siendo “K” la rugosidad absoluta, cuyo valor es de 0,03 mm.
Con los valores obtenidos del número de Reynolds y de la rugosidad relativa se obtiene un coeficiente de fricción de 0,01025.
La pérdida de carga por rozamiento en la tubería en función del caudal es:
La suma de la altura geométrica “Hg” y de las pérdidas por rozamiento en función del caudal “Hf”, proporciona la curva característica de la conducción o curva resistente de la tubería:
Con las necesidades de altura y caudal, el fabricante proporciona una bomba cuya curva motriz pasa lo más próximo posible al punto en cuestión y en la zona de buen rendimiento. La curva motriz de la bomba viene dada por la siguiente expresión:
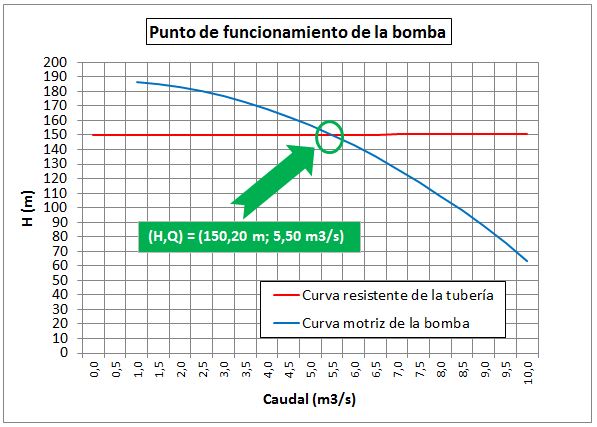
El punto de funcionamiento viene dado por la intersección de ambas curvas y se puede ver en el gráfico siguiente:
Gráfico 1. Punto de funcionamiento. Intersección de la curva resistente de la tubería y de la curva motriz de la bomba.
Según el fabricante, el rendimiento de la bomba seleccionada en el punto de funcionamiento es del 80%, por lo tanto la potencia de la bomba es:
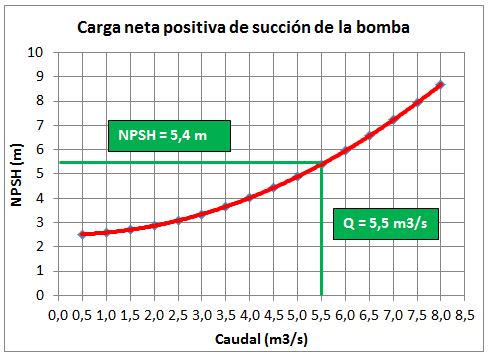
El fabricante también nos proporciona el NPSH (Net Positive Suction Head) de la bomba, tal y como se muestra en la gráfica siguiente:
Gráfico 2. Carga neta positiva de succión de la bomba.
Este valor de la carga neta positiva de succión, nos permite estimar el valor máximo de la altura de aspiración “Ha” con la siguiente fórmula: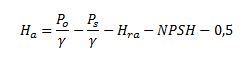
Siendo:
Po/γ: la altura de presión atmoférica (10,33 m),
Ps/γ: la altura de presión de saturación en la instalación hidráulica,
Hra: la caída de presión entre la aspiración y la entrada a la bomba,
El fabricante facilita los valores de “Ps/γ” y de “Hra”, por lo tanto:
Se decide adoptar definitivamente una altura de aspiración de 3 m. Con esta altura no se supera el límite y no se produce cavitación en la bomba.
También se decide colocar otra bomba, idéntica a la anterior, en reserva activa, y para ir utilizándola alternativamente.
5. ANÁLISIS DEL TRANSITORIO HIDRÁULICO. SOBREPRESIONES POR GOLPE DE ARIETE
La parada del grupo motor-bomba debido a una interrupción súbita del suministro eléctrico suele desencadenar un régimen transitorio rápido inercial que requiere tener en consideración las inercias del sistema, es decir, la inercia del grupo elevador rotante (masas rotantes) y la inercia de la columna de agua ascendente a lo largo de la conducción.
Si los cambios de presión y velocidad se producen con gran rapidez (cambios bruscos de las variables hidráulicas) hay que contar con la compresibilidad del agua y con la elasticidad de la tubería, y analizar el problema con las ecuaciones del golpe de ariete.
La celeridad es un valor clave en el cálculo del régimen transitorio y representa la velocidad a la que se propagan las perturbaciones (ondas de presión) en el seno del sistema fluido-conducción. Se calcula a partir de las características de la tubería y del fluido mediante la siguiente expresión:
Siendo:
k’: módulo de compresibilidad del agua (N/m2), ρ: densidad del fluido (kg/m3), e: espesor de la tubería (m), E: módulo de Young (N/m2). Entonces:
A continuación se procede al cálculo de las sobrepresiones por parada del grupo motor-bomba en la tubería de impulsión (golpe de ariete). Se considera que no se produce la separación de la columna líquida, por cavitación, durante el transitorio.
Para realizar la modelación del sistema se ha empleado el software Dyagats 2.0, Diseño y Análisis del Golpe de Ariete en Tubería Simple, desarrollado por la Unidad Docente de Mecánica de Fluidos de la Universidad Politécnica de Valencia (1993) que es aplicable a una tubería simple y que proporciona las envolventes de alturas piezométricas máximas y mínimas, tras resolver las ecuaciones que gobiernan el fenómeno del golpe de ariete. La versión gratuita del programa se puede descargar en la siguiente dirección web:
http://fluing.upv.es/dyagats.php
El programa no simula cavitaciones. No debe aparecer cavitación en el sistema ya que la rotura de la columna líquida no se contempla en la resolución analítica. El hecho de que la línea de piezométricas sobrepase (por debajo) la línea de cavitación significa que la instalación no funcionaría correctamente y hay que proceder a modificar el diseño.
Al realizar el cálculo del régimen permanente se obtienen los siguientes resultados:
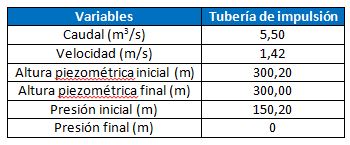Tabla 1. Resultados del cálculo en régimen permanente.
Figura 1. Línea piezométrica de la instalación en régimen permanente.
En la figura siguiente se muestran los valores iniciales (instante t = 0) del caudal y de la velocidad de la bomba, al inicio del transitorio hidráulico, así como los parámetros de cálculo utilizados, es decir, el intervalo de discretización temporal de 0,0401 s y el número de puntos de cálculo (11 nodos) en la tubería.
Figura 2. Valores iniciales (t = 0) para el cálculo del régimen transitorio.
Tras realizar la primera simulación con un valor de la inercia de las masas rotantes del grupo de bombeo de 765 kg.m2 se obtienen las siguientes líneas piezoméricas envolventes:
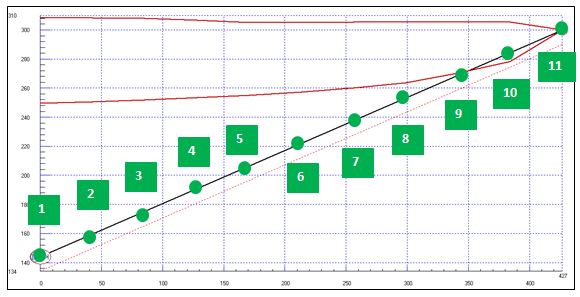Figura 3. Líneas piezométricas envolventes para una bomba con inercia de 765 kg.m2.
En la tabla siguiente se pueden consultar las presiones máximas y mínimas que tienen lugar, así como el instante en que se producen, en cada uno de los nodos en que se ha discretizado la conducción:
Tabla 2. Presiones máximas y mínimas por golpe de ariete (bomba con inercia de 765 kg.m2).
Se observa que la máxima presión tiene lugar en el nodo 1, a los 4,281 s de producirse la interrupción del suministro eléctrico, con un valor de 164,701 m y que la mínima presión tiene lugar en el nodo 10, a los 2,125 s, con un valor de -6,106 m.
Para estudiar la influencia de la inercia de las masas rotantes del grupo de bombeo en la variación del caudal y en las envolventes de presiones máximas y mínimas se han realizado varias simulaciones, con distintos valores de inercia (365, 465, 565, 665, 765, 865, 965, 1065 y 1565 kg.m2) y se han obtenido los siguientes resultados:
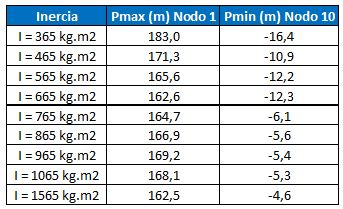Tabla 3. Presiones máximas y mínimas por golpe de ariete para diferentes valores de la inercia de las masas rotantes.
Se observa como para valores de la inercia inferiores a 765 kg.m2, se puede producir cavitación en el nodo 10, ya que la altura de presión relativa es inferior a -10,33 m.
En el gráfico siguiente se pueden ver las envolventes máximas y mínimas de presiones, para los diferentes valores de la inercia:
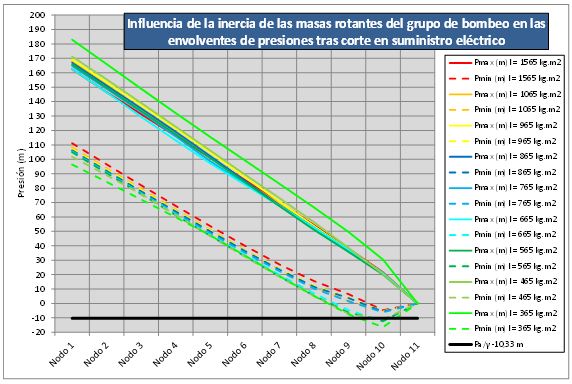Gráfico 3. Influencia de la inercia de las masas rotantes en las envolventes de presiones.
La inercia de las masas rotantes de la bomba también influye en el tiempo en que el caudal en la tubería se hace cero (y por lo tanto en el tiempo de parada), tal y como se aprecia en la gráfica siguiente:
Gráfico 4. Influencia de la inercia de las masas rotantes en el caudal de la tubería (y en el tiempo de parada).
El aumento de la inercia en el grupo de bombeo permite aumentar el tiempo de parada y con ello disminuir los efectos del golpe de ariete. Sin embargo su utilización es limitada al tamaño del volante.
6. PROTECCIONES ANTIARIETE
Una opción para evitar los problemas de cavitación por el golpe de ariete, además de aumentar la inercia de las masas rotantes de la bomba, puede consistir en la instalación de un calderín a la salida del bombeo.
El calderín es un depósito cerrado que tiene aire o un gas inerte bajo presión en la parte superior y un cierto volumen de agua en la parte inferior. Tras la parada de la bomba, el depósito suministra agua a la tubería descomprimiéndose y reduciendo la caída de presión debida al golpe de ariete. Posteriormente, se invierte el sentido del flujo y el agua es de nuevo almacenada en el depósito, comprimiendo el gas.
El software Dyagats proporciona un prediseño de calderín a partir de unos valores de presión máxima y presión mínima. En concreto para unos valores de presión máxima de 185 m y de mínima de 95 m el calderín propuesto tiene una altura de 8,53 m, una sección de 9,14 m2 y un nivel de agua inicial de 1,37 m. El volumen total de calderín es de 77,91 m3 y el volumen de aire inicial en régimen 65,39 m3.
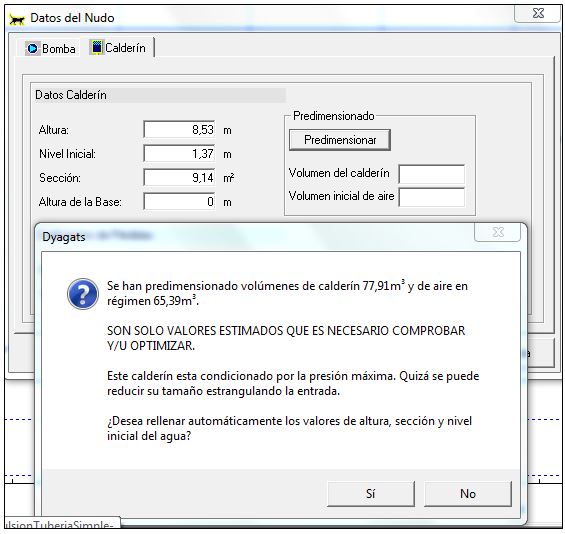Figura 4. Prediseño de calderín con Dyagats 2.0.
A continuación, en el siguiente gráfico, se observa cómo se han resuelto los problemas de depresiones en la zona alta de la tubería de impulsión (nodo 10).
Gráfico 5. Efecto del calderín en la envolvente de presiones máximas y mínimas.
El funcionamiento del calderín viene ilustrado en el gráfico siguiente, en el que se observa la evolución de alturas de agua y de entrada y salida de caudal a lo largo del transitorio hidráulico que tiene lugar en la tubería.
Gráfico 6. Evolución del nivel de agua y del caudal en el calderín durante el transitorio.
La tubería a instalar y todos sus accesorios (piezas especiales, juntas,…) deben ser capaces de resistir una Presión Máxima Admisible (PMA) o presión interna máxima, incluido el golpe de ariete, en servicio y con total seguridad, superior a 187 m, por lo tanto, atendiendo al catálogo del fabricante que ofrece para fundición dúctil PN16 y PN25, nos decantamos por tubería y componentes de presión nominal PN25.
7. CONCLUSIONES
Se ha efectuado el estudio de una impulsión realizando el cálculo del diámetro económico de la tubería, la determinación del punto óptimo de funcionamiento (H, Q) y la elección de la bomba más adecuada, el análisis del golpe de ariete que se produce debido a la interrupción súbita en el suministro eléctrico, el análisis de la influencia de la inercia de las masas rotantes del grupo de bombeo en la variación del caudal y en las envolventes de presiones máximas y mínimas, y por último la propuesta de disponer un calderín, a la salida del bombeo, como protección antiariete, que ha permitido reducir la caída de presión debida al golpe de ariete y eliminar el riesgo de cavitación en la zona alta de la tubería de impulsión.
8. REFERENCIAS BIBLIOGRÁFICAS
Fullana Serra, V., Cabrera Marcet, E. 1977. Análisis simultáneo de las chimeneas de equilibrio y del golpe de ariete por el método de las características. Revista de Obras Públicas Nº 3142.
Mendiluce Rosich, E. 1987. Discrepancias en el cálculo del golpe de ariete. Revista de Obras Públicas. Pág. 575 a 581.
Wylie E. B., Streeter V. L. 1993. Fluid Transients in Systems. Prentice Hall.
Abreu, J.M., et al. 1995. El golpe de ariete en tuberías de impulsión. Comentarios a las expresiones de Mendiluce.
Agüera Soriano, J. 1996. Problemas resueltos de mecánica de fluidos incompresibles y turbomáquinas hidráulicas. Editorial Ciencia 3, S. L.
Agüera Soriano, J. 2002. Mecánica de fluidos incompresibles y turbomáquinas hidráulicas. Editorial Ciencia 3, S. L.
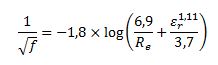
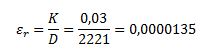
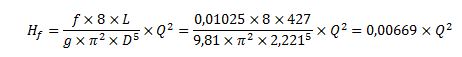
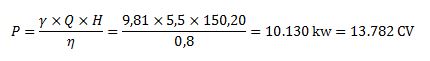
15 Comments
José Díaz Maturana says: 2015/07/03 at 18:39 //
Es interesante el blog
rauhermi says: 2015/07/04 at 10:03 //
Jose, muchas gracias por tu interés.
Saludos cordiales.
Raúl.
Ernesto Cidad says: 2015/12/10 at 19:51 //
Completo y detallado cálculo de una impulsión. Genial que tengas una categoría de “Flujo a Presión”. Intentaré no perderme esos posts.
Gran trabajo y ánimo con el blog y el proyecto Es el Agua.
Ernesto.
rauhermi says: 2015/12/11 at 09:31 //
Ernesto muchas gracias. Pensé que era importante tratar el flujo a presión en régimen transitorio. Una vez al mes suelo publicar un artículo.
Saludos. Raúl.
castor javier garcia alarcon says: 2016/09/15 at 06:12 //
Buenos dias Raul
Muy buen artículo
Soy profesor de Obras Hidráulicas en la universidad Alfonso X el Sabio
¿¿Podria utilizar este articulo para exponerlo a los alumnos en las clases??..por supuesto informando de su autor
un saludo
rauhermi says: 2016/09/15 at 06:48 //
Buenos días Javier, muchas gracias por tu interés. Me alegro que te sea de utilidad el artículo. Encantado de que puedas emplear el citado artículo para exponerlo a los alumnos de la universidad.
Saludos cordiales.
Raúl.
Luiz says: 2018/01/06 at 15:18 //
Hola.
Me gustaría informarle que, en su artículo, la fórmula que atribuye a Colebrook, 1/f^(-1/2) = -1,8*log[6,9/Re + er^(1,11)/3,7], no es la fórmula de Colebrook. Hubo un equívoco suyo. Esta fórmula es la de Haaland (1983), pero escrita de forma equivocada, pues la fórmula de Haaland correcta es: 1/f^(-1/2) = -1,8*log[6,9/Re + (er/(3,7*D))^1,11]. Cordiales saludos. Luiz.
rauhermi says: 2018/01/18 at 10:26 //
Hola Luiz, gracias por el comentario. Los lectores te agradecerán la aportación. Un cordial saludo. Raúl.
Luiz says: 2018/01/30 at 14:01 //
Hola!
Un problema mal resuelto en la ecuación de Colebrook-White, en mi opinión, es el valor de la la rugosidad relativa “εr”. No hay consenso al respecto. Para el mismo material, distintos autores dan valores distintos. En otras palabras, para lo mismo sistema adductor, dos proyetos pueden ser (estar) absolutamente correctos, pero con diferentes diámetros. ¿Cómo ves esto?
Cordiales saludos.
Luiz.
rauhermi says: 2018/01/31 at 10:03 //
Hola Luiz, el caso que planteas es de elevado interés. Si la diferencia entre los diámetros resultantes es significativa y la elección de uno u otro diámetro para la tubería tiene influencia importante en el coste de la instalación (construcción, consumo de energía durante la explotación, etc.) pienso que puede estar justificado recurrir a la modelación física hidráulica. Mediante ensayos de laboratorio se pueden obtener los valores del coeficiente de fricción “f” (fórmula de Darcy–Weisbach de la pérdida de carga por rozamiento en la tubería) para diferentes regímenes hidráulicos y con esos valores se puede analizar qué ocurre con la rugosidad relativa en la fórmula de Colebrook-White.
Saludos.
Raúl.
Ing. Angel Garcia Arzate says: 2019/01/24 at 20:25 //
Excelente post. Hacen falta este tipo de análisis prácticos. En los libros es mucha teoría pero faltan aplicaciones de ingeniería.
rauhermi says: 2019/01/25 at 17:36 //
Hola Ángel, gracias por tu interés en el blog de Es el agua. Me alegro que el artículo te haya resultado útil y práctico. Un cordial saludo.
Norman Joseph Vargas says: 2022/06/27 at 15:11 //
Estimado ing. Raul, mucho me place encontrar personas como ud que tienen la capacidad y el desprendimiento profesional de compartir este tipo de informaciones. Lamento que otras personas le critiquen, cuando no se han atrevido a hacer publicaciones similar a la suya. Hay que tener etica profesional y respeto a aquellos que tienen el valor de publicar. Lo exorto a no sentirse mal por los comentarios anteriores y a seguir con sus publicaciones. Un abrazo.
Norman Joseph Vargas says: 2022/06/27 at 15:15 //
N.B.:
Ingeniero, estoy haciendo un Manual de diseño para sistemas de agua potable, aguas servidas y Pluviales. Puedo incluir su ejercicio en el mismo, poniendo los creditos de su blog y las referencias bibliograficas?
rauhermi says: 2022/07/02 at 16:36 //
Buenas tardes Norman, gracias por su interés y por su valoración.
Sí que puede incluir en su manual el ejercicio citado haciendo referencia al blog y a la bibliografía.
Un cordial saludo.