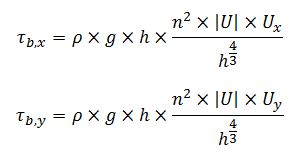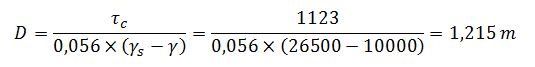Diseño de protecciones de escollera en un tramo de rambla con Iber
Planteamiento del problema
Una rambla se encuentra encauzada en zona urbana mediante muros y tiene una sección transversal rectangular de 100 m de ancho. El caudal empleado para el diseño del encauzamiento fue de 2500 m3/s.
El primer kilómetro de encauzamiento presenta un trazado recto en planta en dirección este-oeste. Los primeros 500 m tienen una pendiente longitudinal del 0,5% y los 500 m siguientes una pendiente longitudinal del 1%.
Seguidamente el encauzamiento presenta una curva girando 90º hacia el sur, con un radio de curvatura de 500 m. A la salida de la curva, el encauzamiento vuelve a presentar una alineación recta en dirección norte-sur en una longitud de 500 m. Tanto en la curva como en el tramo final la pendiente longitudinal continua siendo del 1%.
Tras una avenida reciente se han producido erosiones aguas arriba de la curva, en la propia curva e inmediatamente aguas abajo de la misma. Se plantea proteger con escollera el lecho del tramo de rambla que ha sufrido erosión, dimensionando dicha protección.
Figura 1. Planta con la definición geométrica del encauzamiento de la rambla
Tras abordar el problema en el post anterior haciendo uso de la fórmula de Maynord et al. (1987) aplicable para el diseño de protecciones generales de escollera, se procede a resolver el mismo problema haciendo uso del modelo hidráulico bidimensional Iber.
Construcción del modelo en Iber
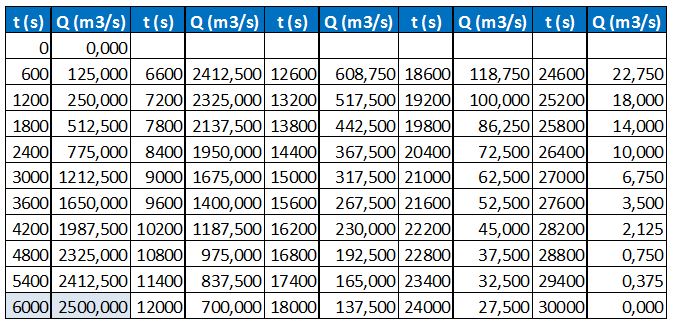
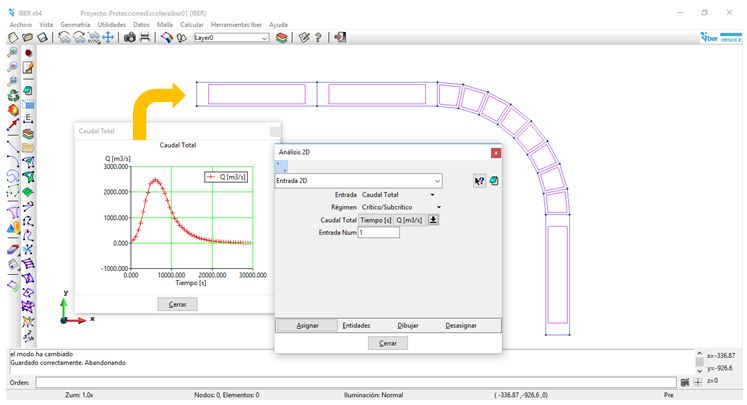
Se ha introducido la geometría del encauzamiento de la rambla en el modelo Iber y se ha aplicado la condición de contorno de entrada correspondiente al hidrograma siguiente en régimen subcrítico:
Tabla 1. Hidrograma para la aplicación de la condición de contorno de entrada al modelo
El hidrograma presenta un caudal máximo de 2500 m3/s en el instante t = 6000 s.
Figura 2. Geometría en Iber y condición de contorno de entrada
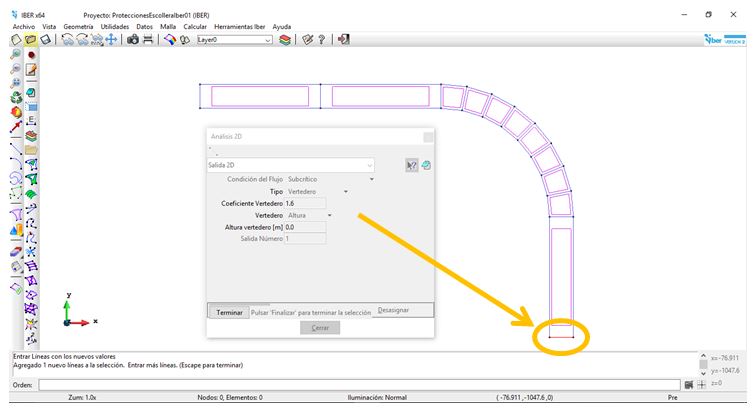
Como condición de contorno se salida aguas abajo en régimen subcrítico se ha considerado una condición tipo vertedero de altura cero y coeficiente de desagüe 1,6.
Figura 3. Condición de contorno de salida
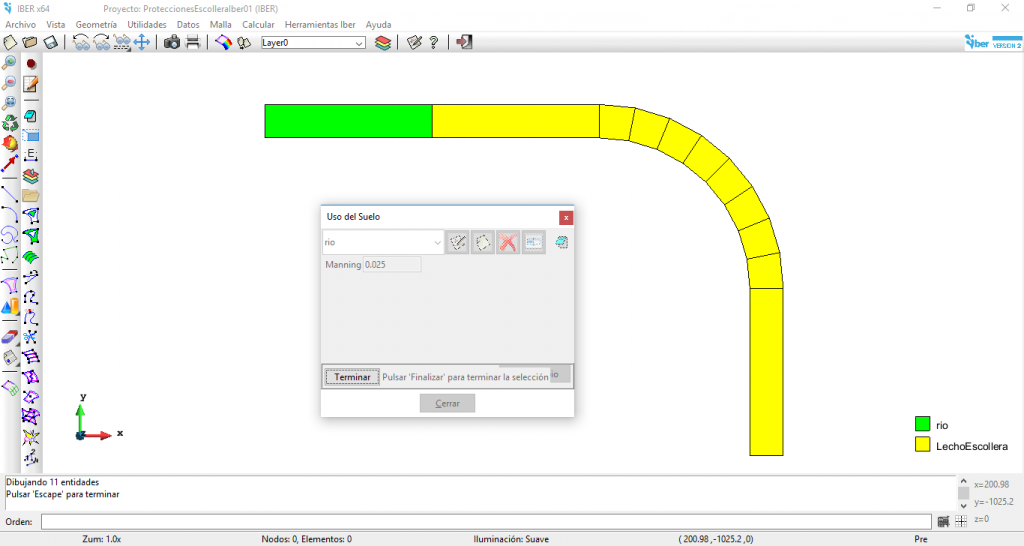
Y en cuanto a las rugosidades, para el primer tramo se ha considerado un valor del coeficiente de rugosidad de Manning de 0,025 y para el resto del encauzamiento 0,043 (correspondiente al tramo a proteger con escollera).
Figura 4. Valores del coeficiente de rugosidad de Manning
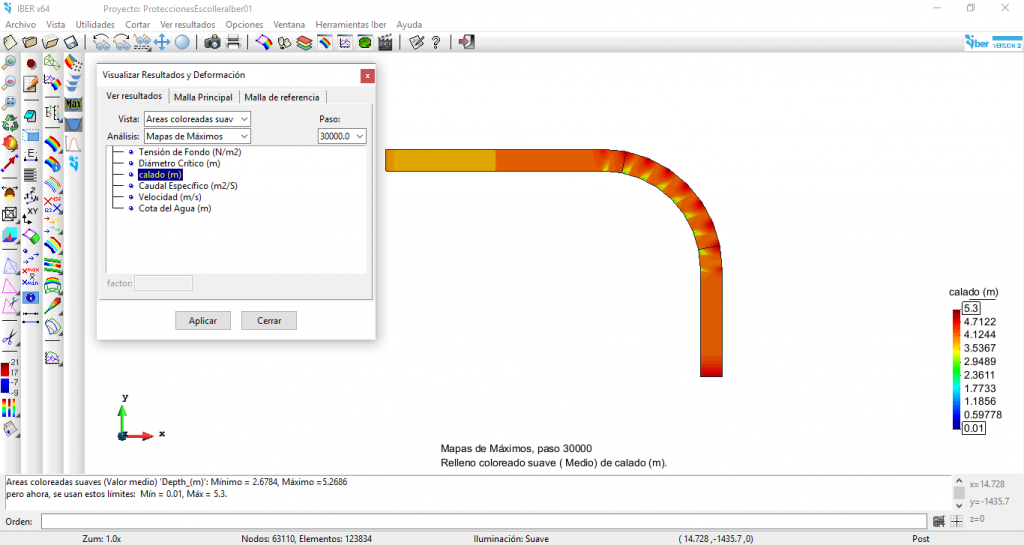
Calados máximos
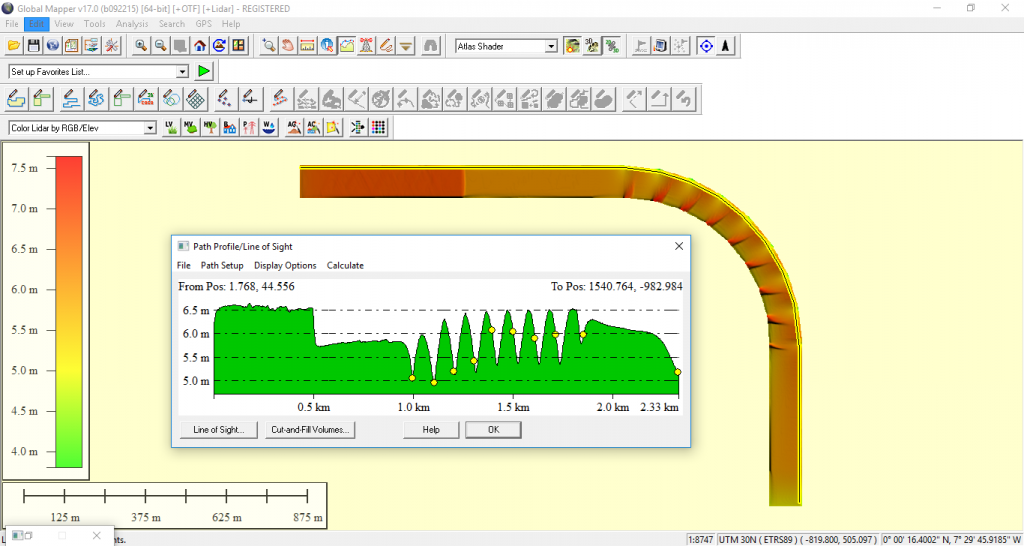
Los calados máximos resultantes en el tramo de rambla tras el tránsito del hidrograma de avenida se pueden observar en las imágenes siguientes:
Figura 5. Calados máximos obtenidos con el modelo Iber
Figura 6. Calados máximos obtenidos en la parte exterior
Figura 7. Calados máximos obtenidos en la parte interior
En la parte exterior del tramo en curva se alcanzan calados próximos a los 5,00 m, mientras que en la parte interior del tramo en curva se alcanzan calados en el entorno de los 4,20 m, lo cual supone una sobreelevación de unos 0,80 m.
Los calados son similares a los obtenidos en el post anterior, en donde se había estimado un calado de 4,30 m en el tramo recto aguas arriba de la curva y una sobreelevación de 0,69 m en la curva, con lo que resultaba un calado máximo en la curva de 4,99 m.
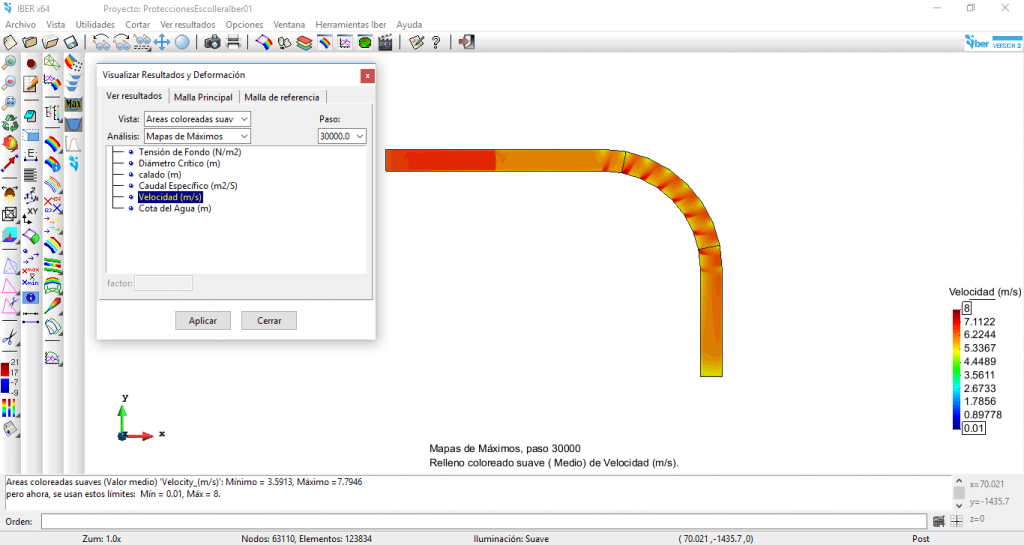
Velocidades máximas
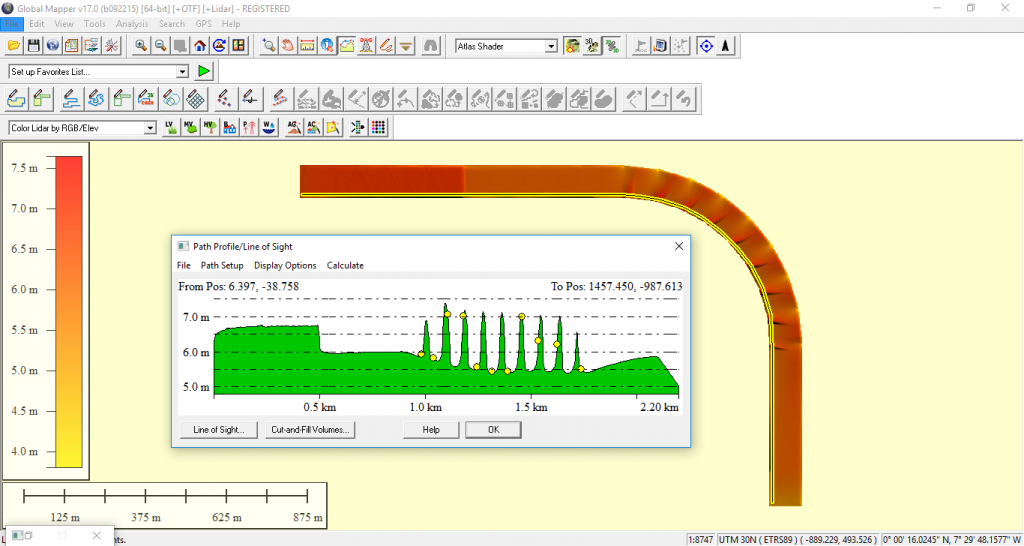
Las velocidades máximas resultantes en el tramo de rambla tras el tránsito del hidrograma de avenida se pueden observar en las imágenes siguientes:
Figura 8. Velocidades máximas obtenidas con el modelo Iber
Figura 9. Velocidades máximas obtenidas en la parte exterior
Figura 10. Velocidades máximas obtenidas en la parte interior
En la parte exterior del tramo en curva se alcanzan velocidades próximas a los 6,50 m/s, mientras que en la parte interior del tramo en curva se alcanzan velocidades en el entorno de los 7,50 m/s.
En el post anterior se había estimado un valor medio de la velocidad de 5,82 m/s. El modelo hidráulico bidimensional representa unas perturbaciones en el tramo en curva que se traducen en variaciones significativas de los calados y de las velocidades.
Tensiones de fondo y diámetros críticos máximos
Tal y como se estudió en el post anterior, la fórmula de Maynord et al. (1987) permite realizar una estimación del diámetro característico de la escollera con el objeto de que no sufra arrastre. La fórmula es válida para elementos con continuidad longitudinal y del lado de la seguridad para protecciones continuas o mantos continuos. Contempla el mecanismo de fallo por arrastre de la escollera por el flujo.
Iber aporta como resultados los valores de la tensión de fondo obtenidos como:
Siendo:
ρ la densidad del agua,
g la aceleración de la gravedad,
h el calado,
n el coeficiente de rugosidad de Manning,
|U| el módulo de la velocidad,
Ux la componente x de la velocidad,
Uy la componente y de la velocidad.
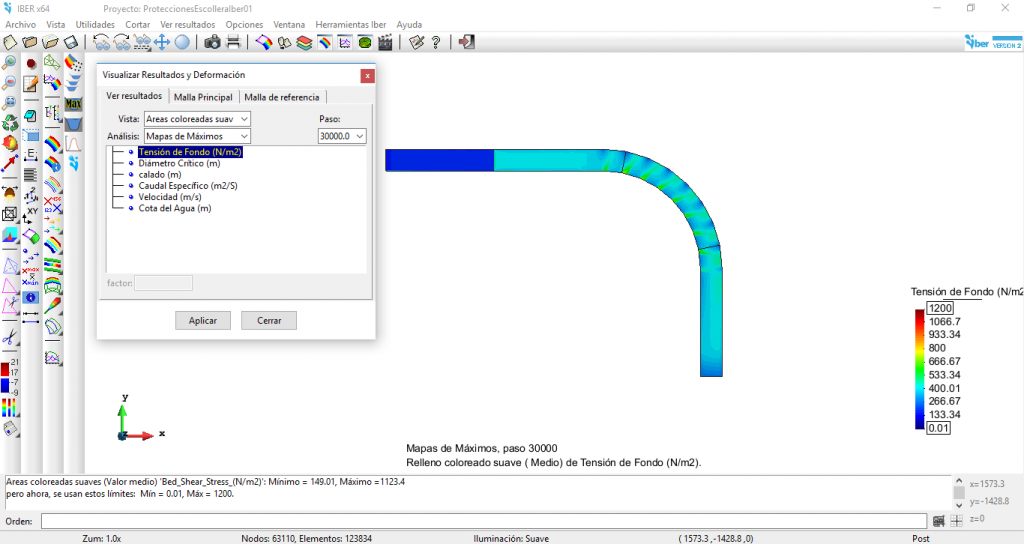
Figura 11. Tensiones de fondo obtenidas con el modelo Iber
El valor máximo de la tensión de fondo que proporciona Iber es de 1123 N/m2.
Haciendo uso de la expresión de Shields (1936) para el cálculo de la tensión crítica:
Siendo:
γs el peso específico de las partículas.
γ el peso específico del agua.
D el diámetro crítico.
Por lo tanto:
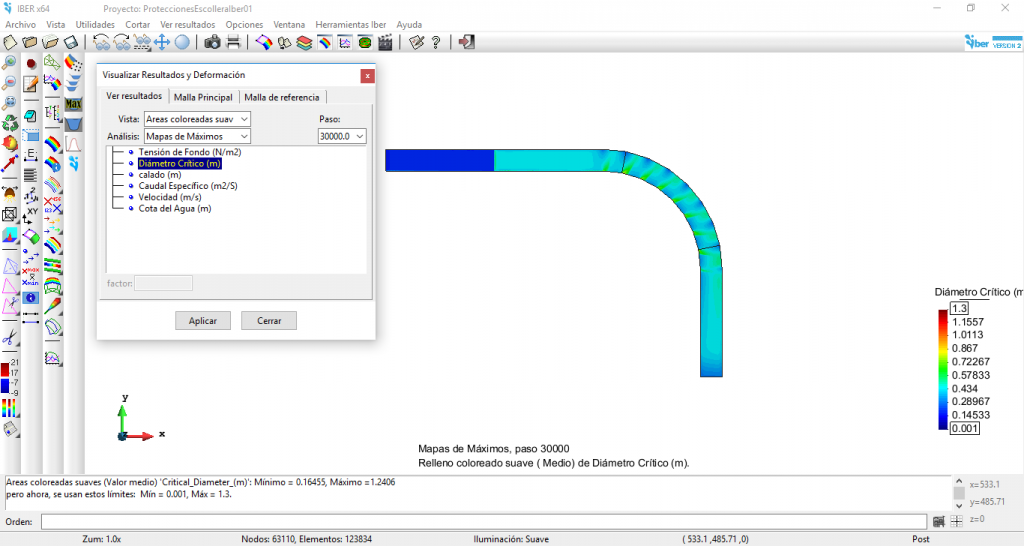
Y como se aprecia en la siguiente imagen Iber también proporciona los valores del diámetro crítico, siendo el valor máximo de 1,241 m.
Figura 12. Diámetros críticos máximos obtenidos con el modelo Iber
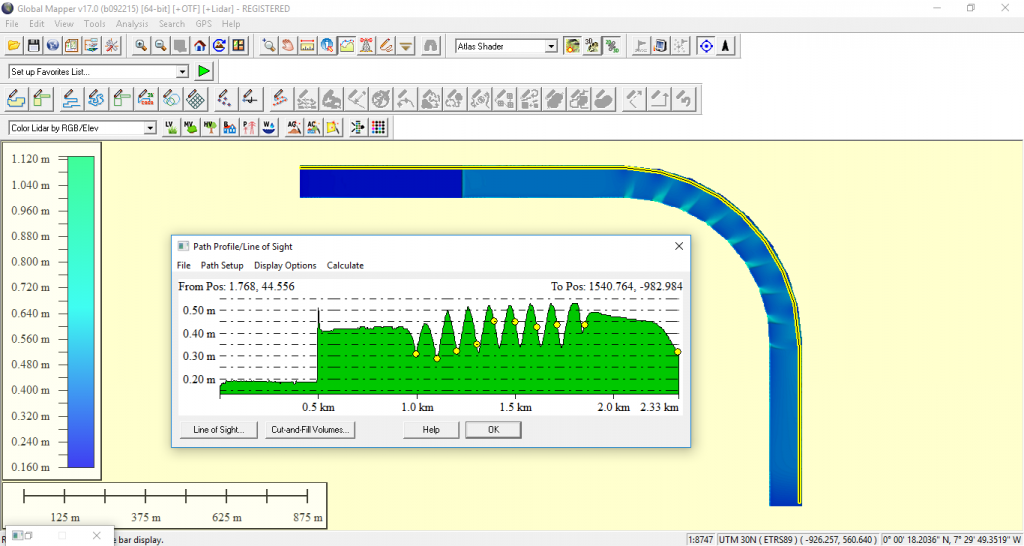
Figura 13. Diámetros críticos máximos obtenidos en la parte exterior
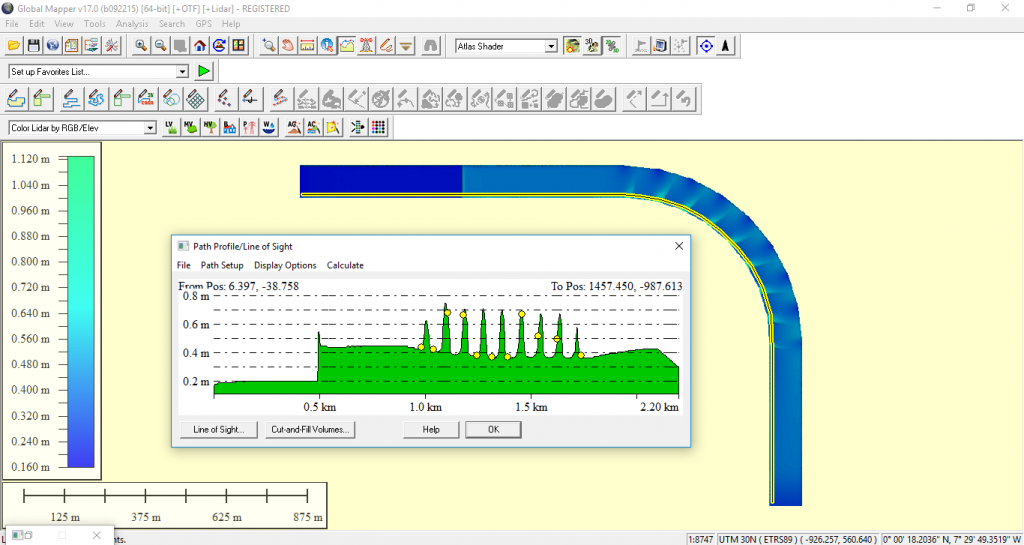
Figura 14. Diámetros críticos máximos obtenidos en la parte interior
En la parte exterior del tramo en curva se alcanzan valores del diámetro crítico de 0,55 m, mientras que en la parte interior del tramo en curva se alcanzan valores en el entorno de los 0,80 m.
En el post anterior se había estimado un valor del D50 para el tramo recto de 0,72 m y de 0,83 m para el tramo en curva.
Por lo tanto, se concluye que las dos metodologías de cálculo proporcionan resultados similares en cuanto al tamaño característico de la escollera de protección para el lecho de la rambla.