¿Es necesario proteger este encauzamiento?
1. INTRODUCCIÓN
En el presente post se lleva a cabo un estudio hidráulico en régimen transitorio con el objeto de diseñar las protecciones necesarias para un encauzamiento.
Se parte del hidrograma de caudal para un periodo de retorno de 500 años y de la geometría del encauzamiento, y se aplica la formulación de la onda dinámica a través del programa Storm Water Management Model (SWMM) de la Environmental Protection Agency (EPA).
Una vez realizado en cálculo hidráulico se diseñan unas protecciones con la finalidad de impedir la erosión de la sección transversal del encauzamiento.
2. HIDROGRAMA DE CAUDAL PARA EL DISEÑO
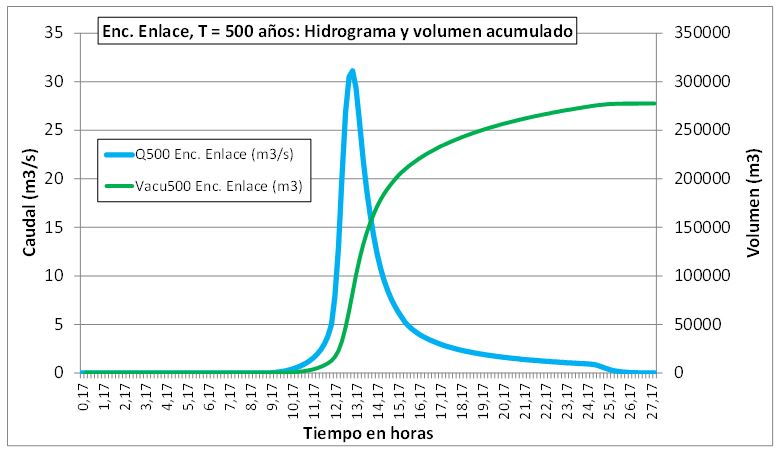
La cuenca vertiente al encauzamiento genera un hidrograma de entrada al mismo, para un periodo de retorno de 500 años, que se puede ver en la gráfica siguiente:
Gráfico 1. Hidrograma de caudal de entrada al encauzamiento y volumen acumulado.
El caudal pico es de 31,10 m3/s y el volumen acumulado 0,277 hm3.
3. FORMULACIÓN DE LA ONDA DINÁMICA
La realización del análisis del régimen transitorio hidráulico que tendrá lugar en el encauzamiento objeto de estudio como consecuencia del hidrograma de 500 años de periodo de retorno, se llevará a cabo mediante la integración numérica de las ecuaciones de Saint Venant, que proporcionan la solución al cálculo del tránsito de una avenida. Téngase en cuenta que los cauces fluviales y las obras experimentan las mayores acciones y transformaciones durante las avenidas.
La ecuación dinámica de Saint Venant se puede escribir como:
Siendo:
S: la pendiente motriz,
x: la abcisa en la dirección del movimiento,
z: la cota del fondo,
y: el calado,
v: la velocidad,
g: la aceleración de la gravedad,
t: el tiempo.
La ecuación de continuidad escrita por unidad de anchura sería:
En donde “q” representa el caudal específico o caudal por unidad de ancho.
Para integrar las ecuaciones de Saint Venant se empleará la formulación de la onda dinámica completa, a través del programa Storm Water Management Model (SWMM) de la Environmental Protection Agency (EPA), ya que con esta metodología, el modelo hidrodinámico permitirá representar el comportamiento de fenómenos tales como remansos, flujos a presión, flujos inversos, etc.
SWMM emplea la ecuación de Manning para establecer la relación entre el caudal que circula por el encauzamiento (Q), la sección del mismo (A), el radio hidráulico (Rh) y la pendiente (S). La ecuación en unidades del Sistema Internacional se expresa como:
Donde n es el coeficiente de rugosidad de Manning.
En el caso del modelo de la onda dinámica la pendiente S se interpreta como la pendiente hidráulica del flujo, pendiente motriz o pérdida de energía por unidad de longitud.
Como se ha comentado, el transporte de agua a través de los conductos y cauces representados en SWMM está gobernado por las ecuaciones de conservación de la masa y de la cantidad de movimiento, tanto para el flujo gradualmente variado como para el flujo transitorio, y que son las ecuaciones de Saint Venant. En este caso se ha decidido resolver las ecuaciones con el modelo hidráulico de transporte de la onda dinámica.
El modelo de transporte de la onda dinámica resuelve las ecuaciones completas unidimensionales de Saint Venant. Estas ecuaciones suponen la aplicación de la ecuación de continuidad y de cantidad de movimiento en las conducciones y la continuidad de los volúmenes en los nudos.
Con este tipo de modelo de transporte es posible representar el flujo presurizado cuando una conducción cerrada se encuentra completamente llena, de forma que el caudal que circula por la misma puede exceder del valor de caudal a tubo completamente lleno obtenido mediante la ecuación de Manning.
El modelo de transporte de la onda dinámica también contempla efectos como el almacenamiento en los conductos, los resaltos hidráulicos, las pérdidas en las entradas y salidas de las conducciones, el flujo inverso y el flujo presurizado.
Se trata de un método de resolución adecuado para sistemas en los que los efectos de resalto hidráulico, originados por las restricciones de flujo aguas abajo y la presencia de elementos de regulación tales como orificios o vertederos, sean importantes. Y esto entra dentro de los casos que nos ocupan.
4. ENCAUZAMIENTOS
A continuación se lleva a cabo el estudio hidráulico necesario orientado al diseño del encauzamiento para un periodo de retorno de 500 años. El encauzamiento da continuidad a una obra de drenaje transversal que atraviesa una autovía. Esta obra de drenaje está formada por dos marcos de hormigón de ancho 4,00 m y alto 2,00 m.
Como premisa se evitará el diseño del encauzamiento en hormigón.
Para dar continuidad a la obra de drenaje transversal constituida por 2 marcos de hormigón de 4,00 m de ancho y 2,0 m de alto se propone un encauzamiento para transportar un caudal punta de diseño de 31,10 m3/s correspondiente al periodo de retorno de 500 años.
Figura 1. Planta del encauzamiento.
En un primer momento se propone como solución un encauzamiento en tierras y escollera con una longitud de 364 m, entre la desembocadura de la obra de drenaje transversal bajo la autovía y la embocadura de la obra de drenaje transversal bajo la carretera existente. Ambas obras de drenaje transversal tienen las mismas dimensiones.
El encauzamiento tiene sección trapezoidal y taludes 1 H: 1 V. En su parte central el ancho de la base es de 6 m y presenta dos transiciones, es decir, un estrechamiento gradual en curva entre la desembocadura de la obra de drenaje transversal bajo la autovía y el tramo central y un ensanchamiento gradual, también en curva, entre el final del tramo central y la embocadura de la obra de drenaje transversal bajo la carretera.
Para estudiar el comportamiento del encauzamiento propuesto se ha construido un modelo con el software SWMM de la EPA analizando el régimen hidráulico transitorio mediante la formulación de la onda dinámica, a partir del hidrograma de entrada que presenta un caudal pico de 31,10 m3/s y un volumen acumulado de 0,277 hm3, para un periodo de retorno de 500 años.
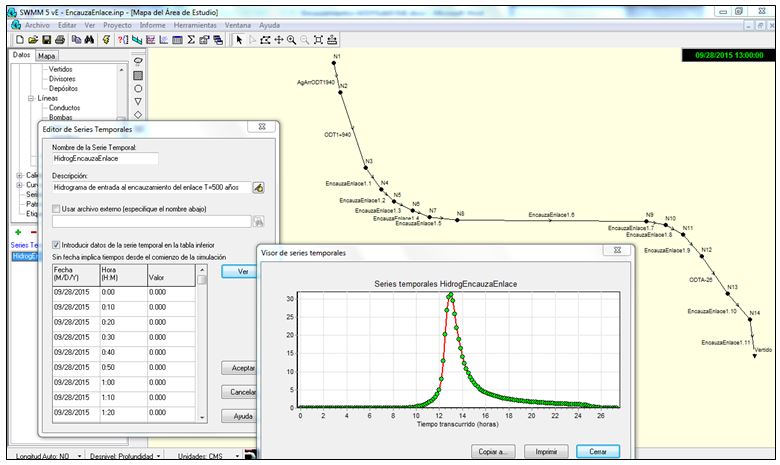
En la siguiente figura se observa el modelo construido y el hidrograma de entrada.
Figura 2. Modelo hidráulico en SWMM e hidrograma de entrada para un periodo de retorno de 500 años en el encauzamiento.
En las siguientes imágenes se puede observar la evolución de la lámina de agua con el paso del tiempo:
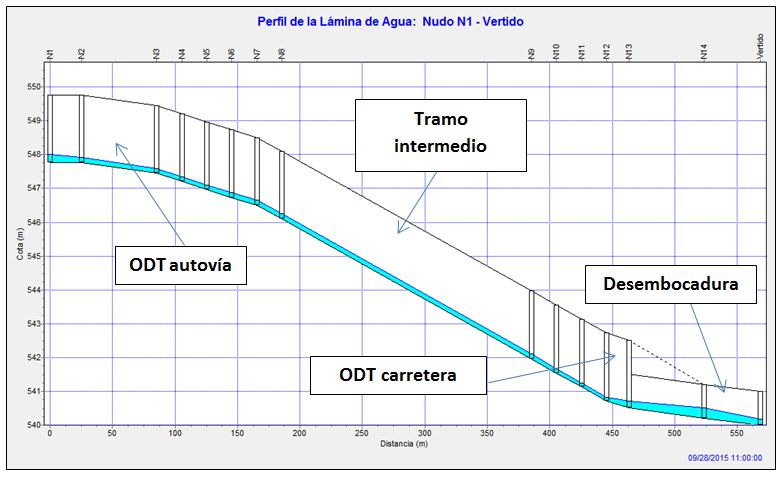
Figura 3. Perfil longitudinal de la lámina de agua en el instante 11:00 h, prácticamente al inicio del hidrograma, para un caudal de 1,31 m3/s.
Se aprecia como para estos primeros caudales el vertido en la desembocadura se produce de forma libre.
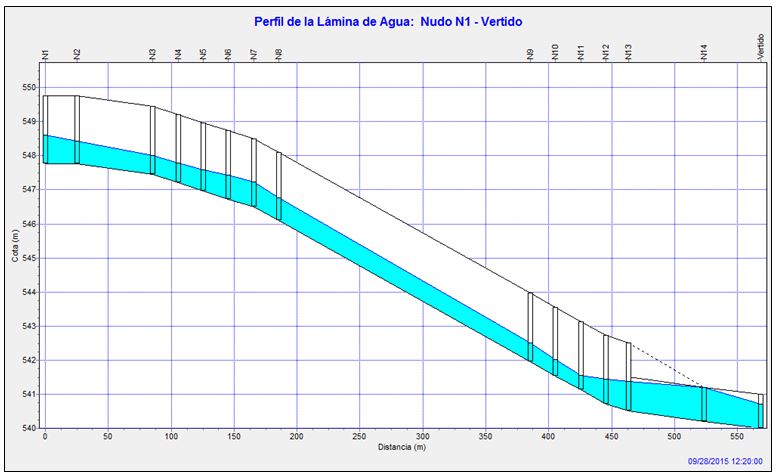
Figura 4. Perfil longitudinal de la lámina de agua en el instante 12:20 h, en la rama ascendente del hidrograma, para un caudal de 12,90 m3/s.
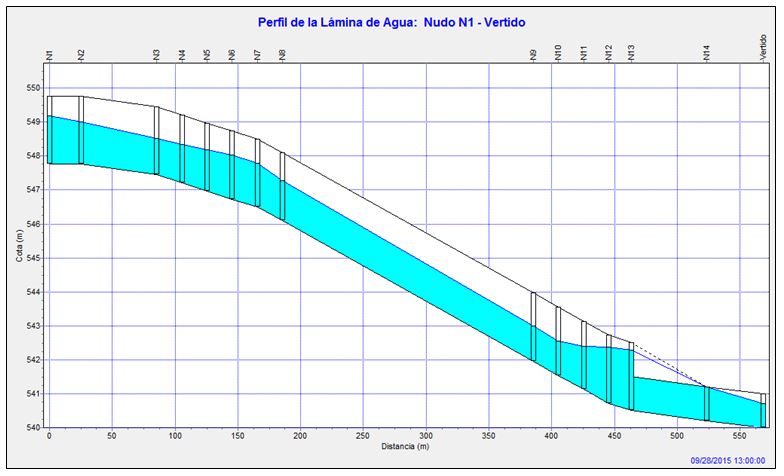
Figura 5. Perfil longitudinal de la lámina de agua en el instante 13:00 h, coincidente con el tránsito del caudal pico de 31,12 m3/s.
Como se aprecia, el resalto hidráulico se produce hacia el final de la rápida y a la salida de la obra de drenaje transversal bajo la carretera. Tanto la entrada como la salida de la obra de drenaje transversal bajo la carretera se deberá proteger convenientemente con escollera.
No se produce la entrada en carga durante el tránsito del caudal pico en ninguna de las obras de drenaje transversales. En la siguiente gráfica se puede observar la evolución de los niveles de agua a la entrada y a la salida de las obras de drenaje transversal:
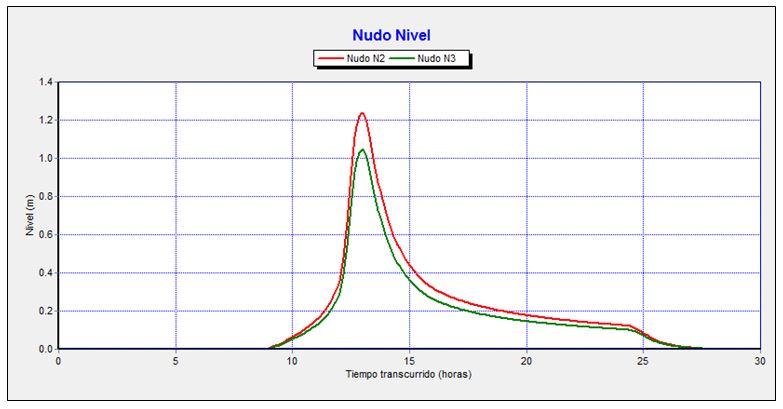
Gráfico 2. Evolución de niveles a la entrada y a la salida de la obra de drenaje transversal bajo la autovía durante el tránsito de la avenida de 500 años de periodo de retorno.
Aguas arriba de la obra de drenaje transversal bajo la autovía el agua alcanza un calado máximo de 1,24 m e inmediatamente aguas abajo a la salida de la ODT el calado máximo sería de 1,05 m.
La velocidad máxima alcanzada en esta obra de drenaje transversal es de 3,40 m/s.
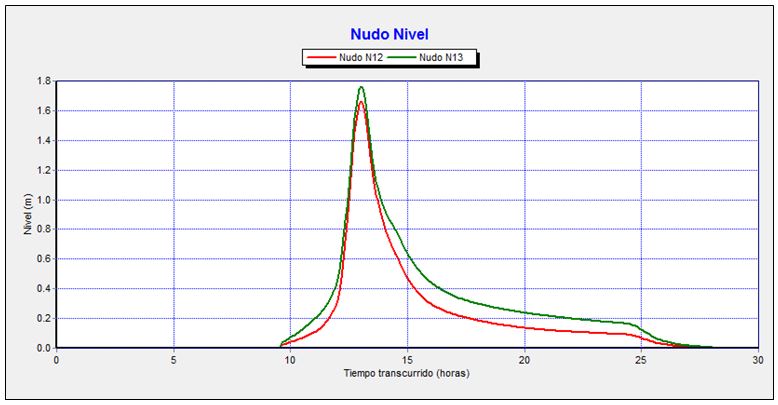
Gráfico 3. Evolución de niveles a la entrada y a la salida de la obra de drenaje transversal bajo la carretera durante el tránsito de la avenida de 500 años de periodo de retorno.
El comportamiento de los niveles en esta obra de drenaje transversal bajo la carretera es contrario al de la obra de drenaje transversal anterior, es decir, aguas arriba de la obra de drenaje el agua alcanza un calado máximo de 1,67 m, menor que el alcanzado a la salida de la citada obra, donde el calado máximo que se alcanzaría sería de 1,77 m, debido al cambio de pendiente y al resalto hidráulico.
La velocidad máxima alcanzada en la obra bajo la carretera es de 2,33 m/s.
A lo largo del encauzamiento la evolución de los niveles sería:
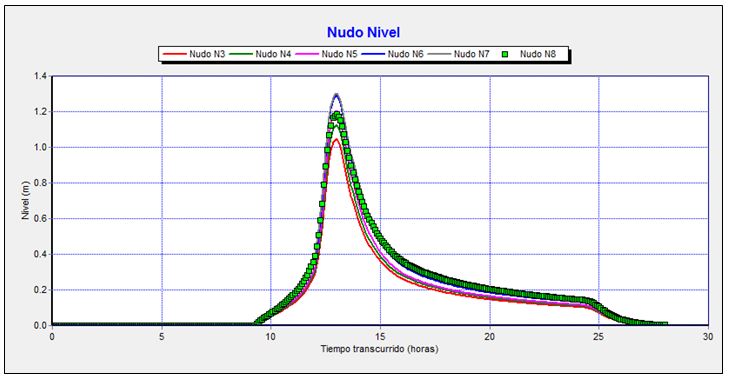
Gráfico 4. Evolución de niveles entre la salida de la obra bajo la autovía y el tramo intermedio del encauzamiento durante el tránsito de la avenida de 500 años de periodo de retorno.
Se observa que a la salida de la obra y durante la primera curva del encauzamiento, los niveles máximos están comprendidos entre 1,05 m y 1,30 m.
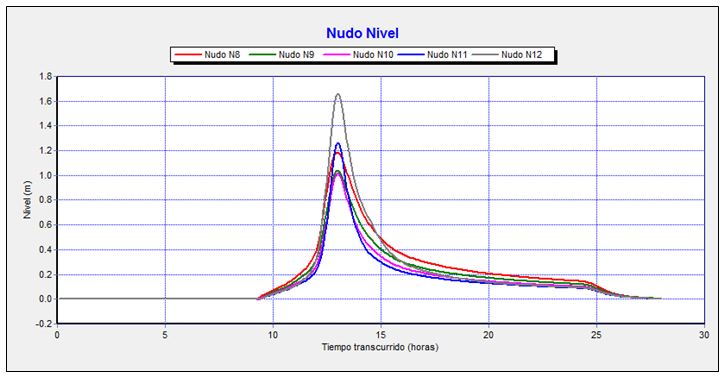
Gráfico 5. Evolución de niveles entre el tramo intermedio del encauzamiento y la obra bajo la carretera durante el tránsito de la avenida de 500 años de periodo de retorno.
Se observa que los niveles van en aumento conforme el agua se aproxima a la obra bajo la carretera, debido al cambio de pendiente existente y al efecto de la forma de la desembocadura, de manera que los niveles máximos van en aumento desde 1,02 m y hasta 1,67 m.
Para que la obra bajo la carretera no entre en carga la sobreelevación por el efecto de la curva no debería ser superior a 30 cm.
Entonces, como:
Siendo:
r: radio de curvatura mínimo,
v: velocidad media en la sección transversal,
B: ancho de la sección,
g: aceleración de la gravedad,
Δz: Sobreelevación entre la orilla exterior e interior de la curva.
Y como la curva proyectada tiene un radio superior a 35 m, se evita la entrada en carga de la obra de drenaje transversal bajo la carretera.
Una recomendación de buena práctica es que el radio de curvatura medio en las curvas fluviales esté comprendido entre 5 y 8 veces la anchura del cauce.
Admitiendo un valor de ancho medio del encauzamiento en la curva de 7 m, el valor del radio debería estar comprendido entre 35 y 56 m.
Por tanto, un radio de curvatura de 35 m estaría justificado en este caso.
En cuanto a la primera curva, a la salida de la obra de drenaje transversal bajo la autovía:
Y siguiendo la recomendación de buena práctica de que el radio de curvatura medio en las curvas fluviales esté comprendido entre 5 y 8 veces la anchura del cauce, admitiendo un valor de ancho medio del encauzamiento en la curva de 10 m, el valor del radio debería estar comprendido entre 50 y 80 m.
Concluyendo que un radio de curvatura de 50 m estaría justificado en este caso.
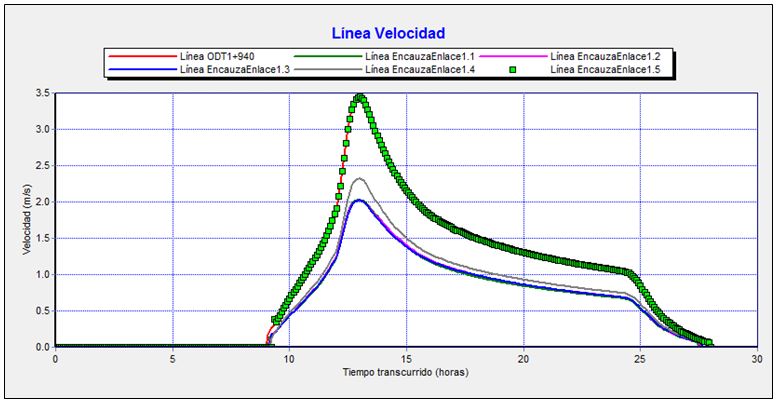
Gráfico 6. Evolución de las velocidades entre la salida de la obra bajo la autovía y el tramo intermedio del encauzamiento durante el tránsito de la avenida de 500 años de periodo de retorno.
Se observa como el flujo se acelera conforme se acerca al tramo de mayor pendiente a la salida de la primera curva. Las velocidades máximas oscilan entre 2,03 m/s a la salida de la obra y 3,45 m/s al inicio de la rampa de mayor pendiente.
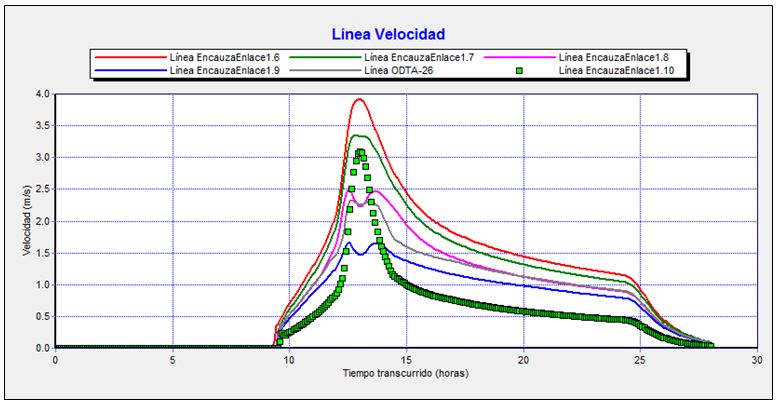
Gráfico 7. Evolución de las velocidades entre el tramo intermedio y la obra de drenaje bajo la carretera durante el tránsito de la avenida de 500 años de periodo de retorno.
Se aprecia como la velocidad máxima tiene lugar hacia el final del tramo de mayor pendiente y se va reduciendo conforme se aproxima a la embocadura de la obra de drenaje transversal bajo la carretera existente.
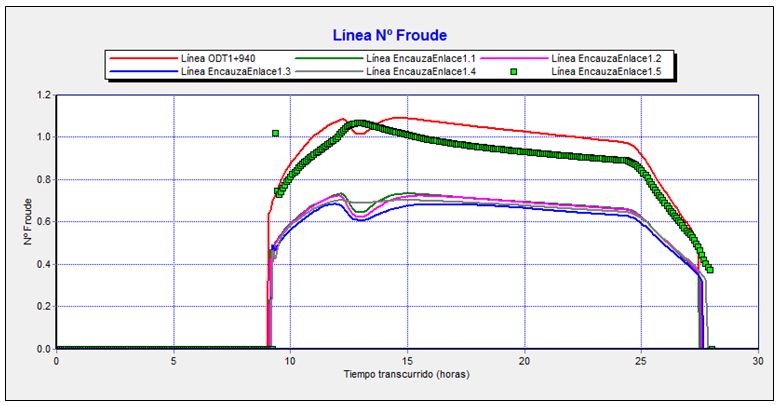
Gráfico 8. Evolución del número de Froude entre la salida de la obra bajo la autovía y el tramo intermedio del encauzamiento durante el tránsito de la avenida de 500 años de periodo de retorno.
La obra de drenaje transversal bajo la autovía y el inicio del tramo de mayor pendiente funcionarían en régimen rápido durante el tránsito de los mayores caudales del hidrograma, con valores del número de Froude ligeramente superiores a la unidad.
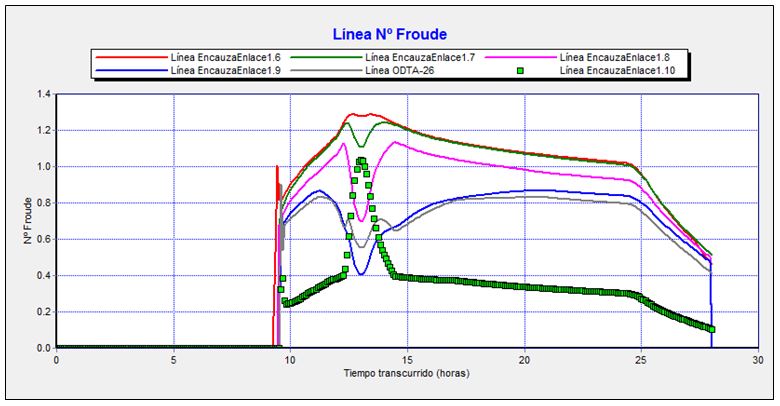
Gráfico 9. Evolución del número de Froude entre el tramo intermedio y el final del encauzamiento durante el tránsito de la avenida de 500 años de periodo de retorno.
Los mayores valores del número de Froude tienen lugar hacia el final del tramo de mayor pendiente y se van reduciendo conforme el agua se aproxima a la salida de la segunda curva y a la embocadura de la obra de drenaje transversal bajo la carretera existente, donde tendrá lugar el resalto hidráulico.
En cualquier caso, al tratarse de valores del número de Froude inferiores a 1,7 estaríamos ante la tipología de resalto hidráulico ondulante.
Una vez que ha transitado por el encauzamiento la punta del hidrograma se irá produciendo el vaciado del mismo. En la siguiente figura se puede ver el perfil de lámina de agua en un instante posterior al paso del caudal pico:
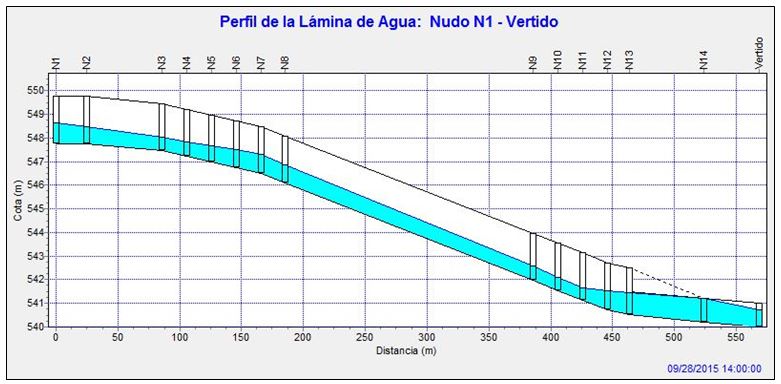
Figura 6. Perfil longitudinal de la lámina de agua en el instante 14:00 h, una hora después de haberse producido el paso del caudal pico, y para un caudal de 14,11 m3/s.
5. PROTECCIONES CON ESCOLLERA
La función de la escollera es impedir la erosión del talud de tierras por la acción de la corriente, a través de su resistencia al arrastre gracias al peso y a la imbricación entre los bloques.
En las curvas se trata de impedir la erosión en la orilla exterior que es la más expuesta a la acción erosiva de la corriente y del flujo en curva. Se trata de defender la región de máxima curvatura, extendiendo la protección hacia aguas abajo de la curva, ya que los mayores calados y erosiones se producen aguas abajo del punto de máxima curvatura.
Pero hay que tener en cuenta que al transformar una orilla erosionable en dura se suele inducir una erosión del fondo del cauce al pie del revestimiento de la escollera. Y a la inversa, si se inmoviliza el fondo de un cauce, se puede inducir una erosión en la orilla.
A continuación se procede al cálculo del tamaño o dimensionamiento de la escollera con el objetivo de determinar un diámetro característico de la escollera que no sea arrastrado bajo unas condiciones hidráulicas determinadas.
Se aplicará una expresión que procede de la experiencia en el proyecto de protecciones de escollera en EE.UU., válida para protecciones generales (no locales) continuas de cauces. Las protecciones discontinuas (traviesas,…) precisan de tamaños mayores.
Para el tamaño D30:
Siendo:
D30: tamaño tal que el 30% del peso del material es menor que él,
y: calado de agua sobre el elemento calculado,
v0: velocidad media en la vertical del elemento,
γ: peso específico del agua (1 T/m3),
γS: peso específico de la escollera (se tomará 2,65 T/m3),
g: aceleración de la gravedad.
Sustituyendo, la expresión queda como:
Siendo F el número de Froude.
En esta última expresión se observa que el tamaño de la escollera es muy sensible a la velocidad.
La formulación presupone un espesor suficiente del orden de 2D30, ya que espesores menores pueden llevar a un fallo de la protección.
En el encauzamiento:
El tamaño característico de la escollera tal que el 30% del peso del material es menor que él debe ser de 0,50 m, y su espesor debe ser mayor o igual de 1 m.
La distribución granulométrica de la escollera debe tener varianza (D84/D16) comprendida entre 1,7 y 5,2.
La tensión tangencial en el fondo de la sección trapezoidal del encauzamiento sería:
Y el tamaño de grano que movilizaría la avenida sería:
La erosión en curvas se puede expresar como un factor multiplicativo del calado medio en recta (ym). La siguiente tabla proporciona estos valores, en función de r/B, siendo r el radio de curvatura en el eje y B la anchura de la superficie libre en el tramo recto e y’ el calado en el lado exterior de la curva:
Tabla 1. Estimación de la erosión en curvas.
La tabla se utiliza para estudiar la erosión potencial en un encauzamiento trazado en curvas. En el cauce de avenidas aplica la erosión en curvas como una erosión general transitoria de una avenida.
Para la curvatura de cauce adoptada en el dimensionamiento de los encauzamientos de r/B=5, se pueden alcanzar erosiones significativas, ya que y’/ym = 1,84.
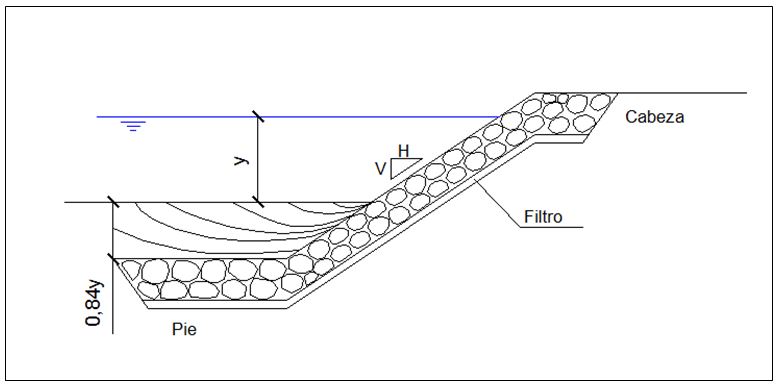
Los taludes de escollera deben continuarse enterrados en el cauce hasta la profundidad adecuada frente a la erosión, para evitar que fallen derrumbándose por haber quedado descalzados debido a la erosión del lecho junto al talud.
Figura 7. Características de la protección de escollera en los encauzamientos.
Para el encauzamiento la cimentación del talud de escollera debe enterrarse 0,84 x 1,50 = 1,26 m.
6. CONCLUSIONES
Para el encauzamiento el radio de curvatura de la segunda curva que se dirige hacia la obra de drenaje situada bajo la carretera existente es adecuado para el correcto funcionamiento del encauzamiento. Sin embargo para la primera curva, proyectada inmediatamente aguas abajo de la obra de drenaje bajo la autovía, se aconseja que tenga un radio de curvatura mínimo de 50 m.
El encauzamiento precisa de taludes de escollera hasta una altura de 1,50 m y la cimentación debe enterrarse 1,25 m.
El tamaño característico de la escollera tal que el 30% del peso del material es menor que él (D30) debe ser de al menos 0,50 m, y se ha de colocar doble capa tal y como se muestra en la Figura 7. La distribución granulométrica de la escollera debe tener varianza (D84/D16) comprendida entre 1,7 y 5,2.
Además se recomienda utilizar escollera en todas las embocaduras y desembocaduras de las obras de drenaje transversal como protección local ante el riesgo especial de erosión.
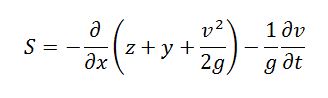
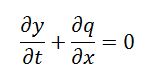



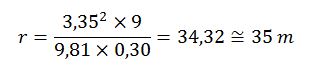


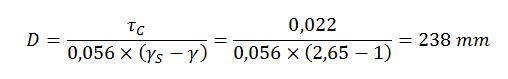

2 Comments
Luis says: 2015/10/29 at 08:39 //
Muy buen artículo Raúl, me alegra que no te hayas limitado a poner los resultados del modelo y ya está, así todo se entiende mucho mejor. Una pregunta ¿Porqué SWMM y no HEC-RAS?
rauhermi says: 2015/10/29 at 16:49 //
Buenas tardes Luis, yo también me alegro que se entienda mejor el contenido y que te resulte de interés. El motivo de emplear SWMM es porque el régimen transitorio hidráulico lleva muchos años probándose con este software y está muy contrastado. Como bien sabrás el cálculo de regímenes transitorios con HEC-RAS es más reciente. Un trabajo interesante sería contrastar los resultados de ambos modelos aplicados a un mismo caso. Saludos.