LAMINACIÓN DE AVENIDAS EN MEDIO URBANO. DEPÓSITOS DE TORMENTAS
1. Introducción
Se desarrolla una metodología para la obtención del volumen de diseño de un depósito de tormentas, cuya función es la de laminar el caudal de la red de saneamiento de aguas pluviales.
2. Estudio pluviológico
Para el dimensionamiento de un depósito de tormentas se calculan las lluvias de proyecto o lluvias sintéticas que se asocian a un cierto periodo de retorno.
La definición de la lluvia para una duración determinada incluirá la cantidad total de precipitación y su distribución espacial y temporal, ya que así lo requiere el método hidrológico del hidrograma unitario que se propone utilizar.
La Agencia Estatal de Meteorología (AEMET) dispone de datos de precipitación en estaciones meteorológicas distribuidas por el territorio nacional, así que se pueden elegir las más próximas al municipio donde se vaya a emplazar el depósito de tormentas.
AEMET dispone de datos de pluviometría desde el año 1920. Los valores estadísticos de las series de precipitación diaria registrados en los pluviómetros se pueden consultar en la dirección siguiente:
http://www.aemet.es/es/serviciosclimaticos/datosclimatologicos/efemerides_extremos
El estudio pluviométrico se realiza con la finalidad de obtener el patrón temporal de la lluvia en el municipio en el que se emplaza el depósito de tormentas. Es conveniente tener en consideración un par de escenarios para la lluvia, es decir, de corta y de larga duración, una vez que se ha elegido el periodo de retorno de diseño.
Para la obtención de las precipitaciones diarias máximas (Pd) en el municipio correspondientes a un período de retorno considerado se propone emplear la metodología propuesta en la publicación “Máximas lluvias diarias en la España Peninsular” de la Dirección General de Carreteras del Ministerio de Fomento.
Obtenido el valor de la precipitación máxima diaria para un periodo de retorno es posible construir la curva Intensidad–Duración–Frecuencia (IDF). Una curva IDF supone una relación entre las intensidades medias máximas esperables, para cada duración de precipitación, con un periodo de retorno considerado.
Debido a la complejidad del proceso y a que no es posible disponer en muchos observatorios de la gran cantidad de datos en forma de hietogramas que son necesarios para la obtención de la familia de curvas IDF de dichos observatorios, diversos autores han buscado relaciones algebraicas que permiten expresar de una manera general la Intensidad Media Máxima en función del intervalo de referencia y del periodo de retorno, a partir de unos datos de pluviometría accesibles como es la precipitación caída en 24 horas.
En España no se ha emprendido un análisis sistemático de curvas Intensidad – Duración – Frecuencia (IDF) para distintas duraciones de lluvia. Sin embargo, en la Instrucción de Carreteras, 5.2.I.C. se propone la siguiente curva IDF sintética:
t: Duración del intervalo al que se refiere It (h)
It: Intensidad media correspondiente al intervalo de duración t deseado (mm/h)
Id: intensidad media diaria correspondiente al periodo de retorno considerado en (mm/h). Se obtiene dividiendo la precipitación total diaria correspondiente a dicho periodo de retorno entre 24 h. Es decir Pd/24 (mm/h).
I1/Id: factor regional de torrencialidad y es el cociente entre la intensidad horaria y la intensidad media diaria, independiente del periodo de retorno y que puede obtenerse para el territorio nacional tal y como muestra la figura siguiente:
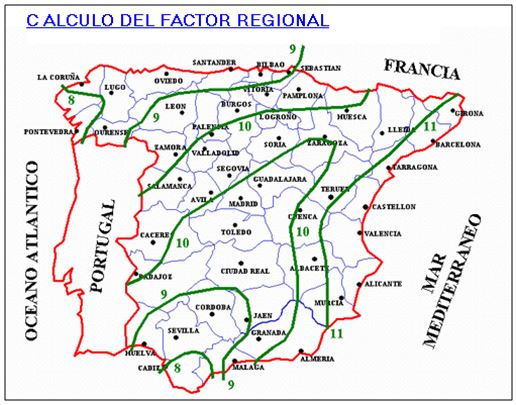 Figura 1. Mapa de España con las isolíneas del factor regional.
Figura 1. Mapa de España con las isolíneas del factor regional.
El método de los bloques alternados permite obtener una lluvia de proyecto a partir de la curva IDF. El hietograma producido por medio de este procedimiento especifica la precipitación en un número n de intervalos de tiempo Δt, para una lluvia de duración total D = n*Δt.
Una vez elegido el intervalo de tiempo Δt, por ejemplo igual a 10 minutos, se toman los datos de intensidad media de precipitación a partir de la curva IDF para duraciones Δt = 10 min. (I10 mm/h), 2Δt = 20min. (I20 mm/h), 3Δt = 30 min. (I30 = mm/h),…, así como la precipitación total obtenida multiplicando las intensidades por las duraciones de lluvia.
Se trata de estimar los intervalos más desfavorables de precipitación, es decir:
Para el tiempo Δt = 10 minutos, la cantidad de lluvia máxima es el dato directo de la curva IDF. Por tanto, tenemos un bloque de lluvia con duración 10 minutos y con intensidad de precipitación la que indica la IDF:
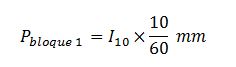 Para un tiempo 2Δt = 20 minutos, la cantidad de lluvia máxima en esos 20 minutos corresponde al dato de la curva IDF, un bloque de lluvia de duración 20 minutos. Pero dentro de esos 20 minutos, admitimos que los 10 minutos más desfavorables corresponden a una precipitación igual al bloque de lluvia calculado en el primer paso. Luego para los segundos 10 minutos, el bloque de lluvia que incluiremos en nuestro hietograma de diseño será uno que produzca una precipitación igual a:
Para un tiempo 2Δt = 20 minutos, la cantidad de lluvia máxima en esos 20 minutos corresponde al dato de la curva IDF, un bloque de lluvia de duración 20 minutos. Pero dentro de esos 20 minutos, admitimos que los 10 minutos más desfavorables corresponden a una precipitación igual al bloque de lluvia calculado en el primer paso. Luego para los segundos 10 minutos, el bloque de lluvia que incluiremos en nuestro hietograma de diseño será uno que produzca una precipitación igual a:
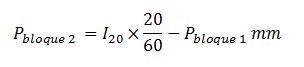 Para un tiempo 3Δt = 30 minutos, la precipitación del tercer bloque de 10 minutos de lluvia será:
Para un tiempo 3Δt = 30 minutos, la precipitación del tercer bloque de 10 minutos de lluvia será:
Estos bloques de lluvia se van distribuyendo de forma alternada, alrededor del bloque de lluvia de mayor intensidad, uno a cada lado (a derechas y a izquierdas).
De esta forma se obtienen los hietogramas de proyecto para una lluvia de corta duración de duración (inferior a 2 horas) y para una lluvia de larga duración (entre 2 y 24 horas de duración) asociados al periodo de retorno de diseño.
El Grupo FLUMEN de Investigación Multidisciplinar en Dinámica Fluvial e Ingeniería Hidrológica (UPC, UB) ha desarrollado un programa que genera la lluvia de diseño mediante la distribución de Bloques Alternados y genera salidas con formato preparado para exportar los resultados a SWMM 5.0
http://www.flumen.upc.es/descarregues.asp
En la figura siguiente se puede ver un ejemplo de hietograma de proyecto:
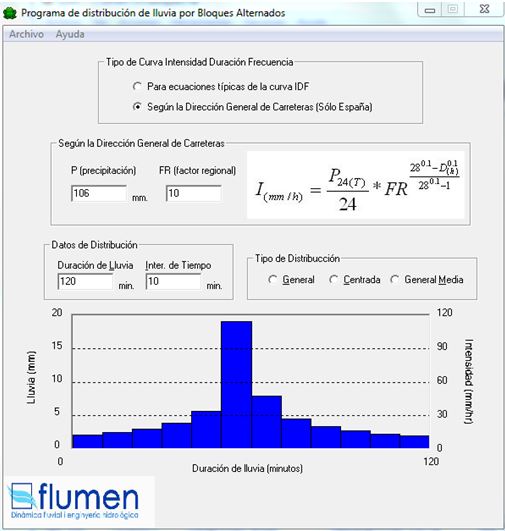 Gráfico 1. Ejemplo de hietograma de proyecto de corta duración para un periodo de retorno 500 años en Alcorcón (Madrid).
Gráfico 1. Ejemplo de hietograma de proyecto de corta duración para un periodo de retorno 500 años en Alcorcón (Madrid).
3. Estudio hidrológico
Un estudio hidrológico puede limitarse a estimar el caudal máximo producido por una lluvia, o bien a definir el hidrograma de caudales que se produce en el punto de desagüe de la cuenca vertiente. La segunda opción es más completa, y necesita un nivel de información previa mayor.
Para dimensionar un depósito de tormentas se propone realizar un estudio hidrológico completo para la obtención de los hidrogramas de caudales asociados a los escenarios de partida con una lluvia de corta duración y con una lluvia de larga duración.
En primer lugar se procede a estimar la fracción de lluvia caída que se va a transformar en escorrentía superficial, es decir, lo que se denomina lluvia neta, a base de restar de la lluvia total caída las pérdidas de precipitación que se producen. Dado el carácter urbano de las cuencas de estudio, las pérdidas de precipitación tienen un peso menor que en cuencas con terreno natural.
La cubierta vegetal suele ser escasa por lo que la intercepción de la vegetación es despreciable. La evapotranspiración también puede desestimarse dado el corto espacio de tiempo de estudio. Solamente pueden tener una cierta influencia la infiltración, en función de la presencia de suelo permeable, y las pérdidas por almacenamiento en depresiones, charcos, puntos bajos, etc.
En la medida que las pérdidas sean menos significativas, será más correcta la asociación entre periodos de retorno de lluvias y periodos de retorno de caudales de escorrentía. De hecho se suele admitir que los caudales de escorrentía superficial que se van a calcular a partir de las lluvias de proyecto tienen el mismo periodo de retorno que éstas.
La infiltración constituye generalmente el factor más importante de las pérdidas. La capacidad de infiltración de un terreno depende del tipo de suelo existente, del uso del terreno, de la pendiente del mismo, del grado de humedad previo del suelo, de la duración e intensidad de la lluvia, etc.
La capacidad de almacenamiento del suelo, que depende de la porosidad, del espesor y de la humedad del suelo es determinante al inicio de la tormenta, aunque una vez que se ha alcanzado la saturación del terreno, la infiltración es igual a la permeabilidad del estrato inferior.
El proceso de infiltración es complejo debido al comportamiento del estrato superficial del terreno, normalmente en condiciones no saturadas, siendo objeto de estudios de detalle por especialistas. La variabilidad espacial de la capacidad de infiltración del suelo añade un grado de dificultad adicional ya que los datos de campo se estiman mediante ensayos en pequeñas porciones del terreno. Además es notable la dispersión existente en los datos experimentales obtenidos mediante ensayos de infiltración in situ.
Debido a que el proceso de estimación de pérdidas presenta naturaleza empírica, los modelos de cálculo comerciales de redes de drenaje incorporan diversos métodos de estimación de las pérdidas de precipitación.
Los métodos más empleados en la evaluación de las pérdidas y la obtención de lluvia neta son:
1) El método de Horton (1940),
2) El método de Holtan (1971),
3) El método de la pérdida inicial y constante en el tiempo,
4) El método del Soil Conservation Service de los Estados Unidos (S.C.S., 1972).
Para la estimación de la lluvia neta se propone emplear el método del Soil Conservation Service (S.C.S., 1972). Este método asume la existencia de un umbral de escorrentía (Po), por debajo del cual las precipitaciones no provocan escorrentía.
Este valor actúa como una intercepción inicial antes de evaluar que una parte de la precipitación escurre superficialmente (E) y que parte es retenida en el terreno (R).
La ecuación que define la relación precipitación escorrentía en este método es la siguiente:
R: La fracción de lluvia retenida por el terreno (mm)
S: La máxima retención posible (mm)
E: La fracción de lluvia que se transforma en escorrentía superficial (mm)
P: La precipitación bruta (mm)
Po: El umbral de escorrentía (mm)
En cada instante la retención sería:
![]() De los análisis empíricos realizados por el S.C.S. resultó la siguiente relación entre Po y S:
De los análisis empíricos realizados por el S.C.S. resultó la siguiente relación entre Po y S:
![]() Combinando las ecuaciones anteriores es posible obtener la fracción de lluvia que se transforma en escorrentía superficial (E) en función de la lluvia bruta (P) y del umbral de escorrentía (Po):
Combinando las ecuaciones anteriores es posible obtener la fracción de lluvia que se transforma en escorrentía superficial (E) en función de la lluvia bruta (P) y del umbral de escorrentía (Po):
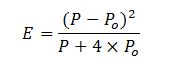 El valor del umbral de escorrentía (Po) en una determinada cuenca y para unas condiciones dadas de humedad es función de la capacidad de infiltración del suelo, del uso del suelo y de la pendiente del terreno.
El valor del umbral de escorrentía (Po) en una determinada cuenca y para unas condiciones dadas de humedad es función de la capacidad de infiltración del suelo, del uso del suelo y de la pendiente del terreno.
Para la estimación del umbral de escorrentía en zona urbana se pueden emplear las Normas para Redes de Saneamiento del Canal de Isabel II (2006). En el Anexo 4 Cálculo del caudal de aguas pluviales se propone la siguiente expresión para el cálculo del coeficiente de escorrentía:
C: El coeficiente de escorrentía medio de la cuenca.
Pd: La precipitación total diaria correspondiente a un período de retorno T, en mm.
Po: El umbral de escorrentía o valor de la precipitación acumulada por debajo del cual no se produce escorrentía, en mm.
Por otra parte, la Normativa para Obras de Saneamiento de la Ciudad de Valencia (2004) propone diferentes valores del coeficiente de escorrentía según el tipo de superficie, tal y como se muestra en la tabla siguiente:
|
Tipo de superficie |
Coeficiente de escorrentía |
|
Áreas pavimentadas |
0,95 |
|
Áreas urbanas |
0,85 |
|
Áreas residenciales |
0,50 |
|
Áreas no pavimentadas |
0,20 |
Tabla 1. Coeficiente de escorrentía según el tipo de superficie.
Una vez obtenido el umbral de escorrentía se procede al cálculo de la lluvia neta (E) resultante, tanto para el escenario de corta duración, como para el de larga duración. A continuación se muestra un ejemplo de hietograma de proyecto de corta duración y la lluvia neta asociada:
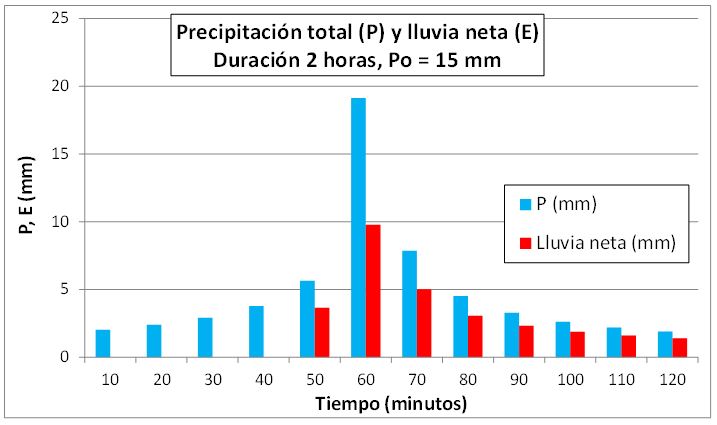 Gráfico 2. Hietograma de proyecto y lluvia neta de corta duración.
Gráfico 2. Hietograma de proyecto y lluvia neta de corta duración.
El proceso de transformar la lluvia neta en caudal se abordó en los albores de la Hidrología Urbana mediante los mismos conceptos empleados en estudios hidrológicos de cuencas rurales. El método más utilizado en dichos estudios es el hidrograma unitario y ese es el primero de los métodos que se emplearon.
La teoría del hidrograma unitario introducida por Sherman (1932) es la más utilizada para transformar el hietograma neto en hidrograma de escorrentía superficial de la cuenca. Se entiende por hidrograma unitario la respuesta en caudal de la cuenca, ante una lluvia neta de valor unidad (1 mm) uniformemente repartida por toda la cuenca.
Más tarde Nash y Dooge (1959) reformularon el concepto, generalizando el concepto de hidrograma unitario como el hidrograma resultante de un impulso de lluvia efectiva unitaria distribuido uniformemente sobre la cuenca y constante durante una unidad de tiempo. El hidrograma unitario instantáneo así definido considera que la transformación lluvia – caudal es la de un sistema lineal e invariable en el tiempo.
En general, se suele referir a una duración cualquiera D, es decir, el hidrograma unitario se define especificando la duración D de la lluvia neta que lo produce, por lo que tenemos un hidrograma como el indicado en la figura siguiente.
 Figura 2. Concepto de hidrograma unitario.
Figura 2. Concepto de hidrograma unitario.
Las propiedades más importantes en la aplicación del hidrograma unitario son:
1) Linealidad en la respuesta. Si un hidrograma H es la respuesta en caudales a una lluvia I1, para una lluvia doble, igual a 2I1, la respuesta en caudal de la cuenca es 2H.
2) Aditividad de la respuesta. La respuesta de un suceso de lluvia I1 más I2, es igual a calcular primero la respuesta en caudal ante una lluvia I1, después la respuesta en caudal ante una lluvia I2, y sumar finalmente los dos hidrogramas de respuesta.
Conocido el hidrograma unitario de duración D, las propiedades anteriores permiten obtener el hidrograma correspondiente a una lluvia cualquiera, descomponiendo la citada lluvia en intervalos de tiempo de duración D.
La segunda propiedad presupone que la respuesta de la cuenca es igual al principio que al final de la lluvia. Si bien eso no es estrictamente cierto, se acepta como hipótesis que simplifica mucho su empleo. El hidrograma unitario es el procedimiento más empleado en el estudio hidrológico de cuencas naturales. La bondad del método radica en que el hidrograma unitario sea representativo de la realidad de la cuenca. Y para ello, debe obtenerse a partir de medidas de campo, de las que se pueda extraer el hidrograma unitario. No es sencilla su extracción, dado que asegurar que la lluvia sea uniforme no es fácil, o tampoco que se cometan mínimos errores de medida de caudal o precipitación. La alternativa es recurrir a hidrogramas unitarios sintéticos, es decir, aproximaciones al hidrograma unitario basadas en datos simplificados de la cuenca, como el tiempo de concentración, etc.
En general en el ámbito de la hidrología urbana se prefiere optar por metodologías que no incluyan la necesidad de determinar un tiempo de concentración a priori, apareciendo dicho concepto con posterioridad como un valor medio de la cuenca.
El método más empleado sigue siendo el hidrograma del S.C.S. en su versión adimensional o triangular, que depende tan sólo del valor del tiempo de concentración.
El hidrograma se basa en un hidrograma adimensional obtenido tras analizar un elevado número de hidrogramas unitarios de cuencas rurales de reducido tamaño y obtener unos valores medios.
Un hidrograma adimensional es un hidrograma unitario en el cual tanto el caudal como el tiempo se expresan como cociente respecto al caudal punta (Qp) y tiempo punta (tp) respectivamente., con lo que se elimina el efecto del tamaño de la cuenca y gran parte del efecto de la forma de dicha cuenca.
El hidrograma unitario adimensional propuesto se encuentra tabulado a continuación:
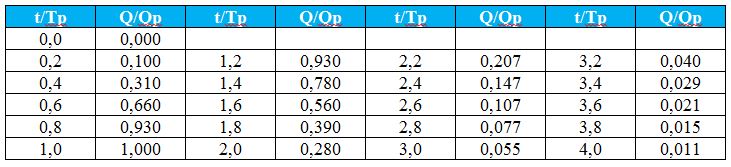 Tabla 2. Hidrograma unitario adimensional del S.C.S.
Tabla 2. Hidrograma unitario adimensional del S.C.S.
El caudal punta se calcula como:
Qp: El caudal punta en m3/s,
A: El área de la cuenca en Km2,
Tp: El tiempo al pico en horas.
El tiempo al pico se puede calcular a partir del tiempo de desfase a la punta (Tdp), como:
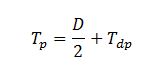 Y el tiempo de desfase a la punta se obtiene a partir de la duración del intervalo de discretización “D” del hietograma a adoptar en la aplicación del método con la expresión:
Y el tiempo de desfase a la punta se obtiene a partir de la duración del intervalo de discretización “D” del hietograma a adoptar en la aplicación del método con la expresión:
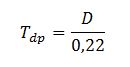 Si por ejemplo se adopta D = 10 minutos (0,17 h)
Si por ejemplo se adopta D = 10 minutos (0,17 h)
Entonces, Tdp es 0,76 h y Tp 0,84 h.
Con esta metodología el hidrograma de caudal que se obtiene se puede ver en el siguiente gráfico:
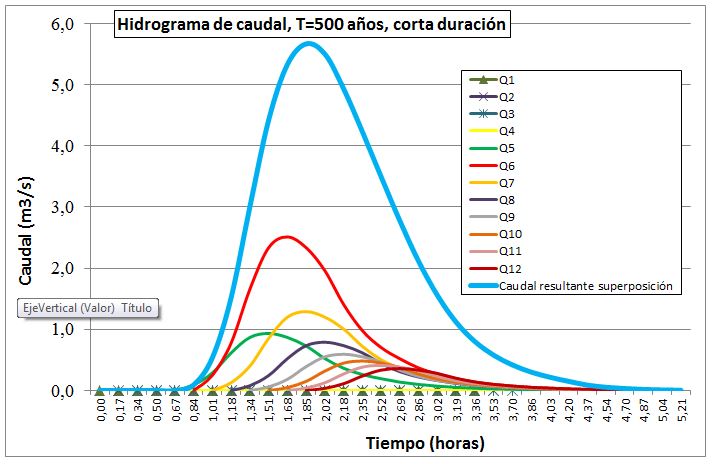 Gráfico 3. Ejemplo de Hidrograma de caudal para el cálculo del volumen de diseño del depósito.
Gráfico 3. Ejemplo de Hidrograma de caudal para el cálculo del volumen de diseño del depósito.
4. Consideraciones sobre la eficiencia de captación de la escorrentía superficial
El proceso de transformación lluvia–escorrentía en zona urbana presenta una serie de particularidades en relación al mismo proceso en un terreno natural. La gran superficie impermeable presente influye en la generación de escorrentía reflejada en términos de caudal especifico (caudal / superficie de la cuenca) y la existencia de una red de drenaje artificial con puntos localizados de entrada de agua en la red condiciona el esquema de cálculo de los caudales de diseño.
Los periodos de retorno que se suelen considerar en zonas urbanas están comprendidos entre 5 y 25 años. Como orden de magnitud se puede indicar que en poblaciones urbanas, para lluvias de periodo de retorno de 10 años se llegan a evaluar caudales específicos similares a los obtenidos en cuencas naturales para lluvias de 500 años de periodo de retorno.
La importancia de la distribución espacial de la precipitación depende del tamaño de la cuenca. Para cuencas pequeñas la distribución habitual que se considera es la uniforme. Yen y Chow (1969) concluyeron que una tormenta en movimiento produce caudales punta similares a los que produciría una tormenta equivalente, pero de tipo estacionario. Sin embargo, los volúmenes de hidrograma sí que pueden variar de manera más significativa por lo que en estudios de depósitos de retención, como es el caso que nos ocupa, donde el volumen de hidrograma es determinante para el diseño, se puede indicar que la metodología podría llegar a sobreestimar el volumen.
Con el estudio hidrológico se ha determinado la cantidad de agua que se transforma en escorrentía superficial para cada uno de los escenarios de partida.
Es importante considerar que los cálculos para la laminación del depósito parten de la hipótesis de que todo el volumen de agua de escorrentía superficial generado se introduce en la red de saneamiento, es decir que los elementos de captación (imbornales, rejas, etc.) tienen una eficiencia del 100%. La realidad demuestra que las eficiencias son inferiores. Por tanto, sería interesante analizar este hecho más en profundidad de cara al diseño definitivo de la red de saneamiento para evacuar los caudales evaluados y para el diseño definitivo del depósito de tormentas, para que las dimensiones de la red y del depósito mantengan una coherencia.
Los caudales de escorrentía deben introducirse en la red de drenaje en los puntos de captación previstos.
Los fabricantes y proveedores proporcionan numerosos datos sobre el comportamiento estructural de las rejas de los sumideros, pero no lo suelen hacer sobre su capacidad hidráulica para la captación de caudales.
Se denomina eficiencia de captación de la reja al cociente entre el caudal interceptado realmente y el caudal de paso por el área contributiva correspondiente de la calle.
La eficiencia del elemento de captación depende del caudal de agua circulante, de la pendiente longitudinal y de la pendiente transversal de la calle.
En la Escuela de Ingenieros de Caminos, Canales y Puertos de la Universidad Politécnica de Cataluña se han realizado ensayos de laboratorio para distintas tipologías de rejas de captación para una calle de 3 metros de anchura con un rango de pendientes longitudinales entre 0 y 10 por ciento y de pendientes transversales entre 0 y 4 por ciento. Se ha comprobado que para valores de caudales circulantes inferiores a 0,05 m3/s la eficiencia de los elementos de captación alcanza valores entre el 60 y el 80 por ciento. Para caudales superiores la eficiencia puede caer a valores del 40 por ciento e incluso inferiores.
Para el dimensionamiento del depósito de tormentas se puede admitir como hipótesis que los elementos de captación de la red de saneamiento tienen una eficiencia comprendida entre el 60 y 80 %, lo que equivale a decir que de todo el volumen de escorrentía superficial, una fracción comprendida entre el 20 y el 40% no va a entrar en la red de saneamiento de aguas pluviales y por tanto no va a acabar entrando en el depósito de tormentas.
5. Análisis de la laminación para el cálculo del volumen de diseño del depósito de tormentas
A continuación se muestra un ejemplo de análisis de la laminación de un depósito de tormentas, en el que se parte de un hidrograma de entrada y una regla de operación de desagüe que tiene en cuenta que el caudal máximo de salida es de 1 m3/s. Haciendo en balance de entradas menos salidas a lo largo del tiempo es posible obtener la evolución temporal del volumen de depósito necesario y por tanto el volumen de diseño, que se corresponde con el volumen máximo tal y como se ve en el gráfico siguiente:
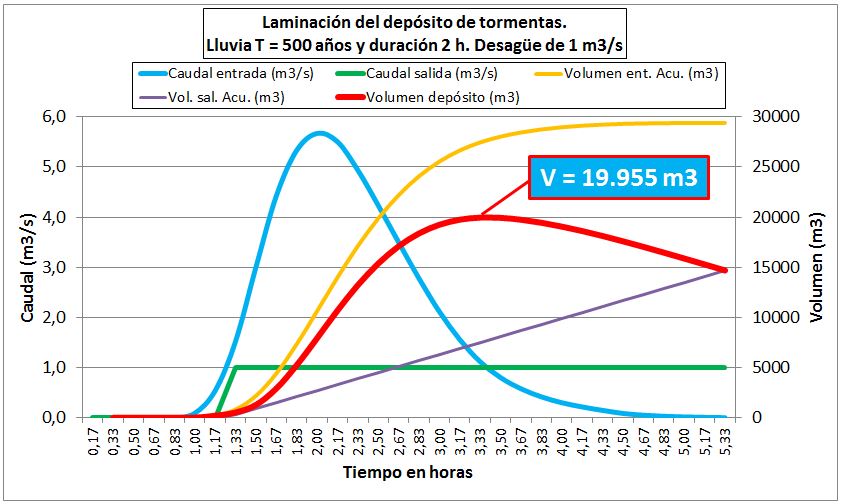 Gráfico 4. Ejemplo de la laminación de un depósito de tormentas para el cálculo del volumen de diseño.
Gráfico 4. Ejemplo de la laminación de un depósito de tormentas para el cálculo del volumen de diseño.

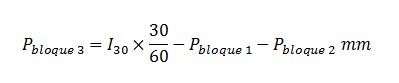
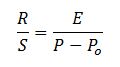
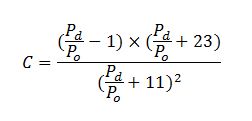
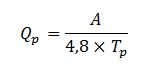
17 Comments
Miguel Cabrera says: 2014/03/31 at 11:17 //
Felicidades por este genial artículo que me ha ayudado a familiarizarme con este tema del que, hasta ahora, no tenía apenas conocimiento.
Gracias!
rauhermi says: 2014/04/01 at 05:31 //
Muchas gracias por tu interés Miguel. Me alegro que el artículo te haya resultado de utilidad. Saludos cordiales. Raúl.
FToledano says: 2014/04/01 at 16:05 //
Te felicito por este artículo y por los que llevas publicados. Te estiy siguiendo con mucho interés y seguramente habrá muchos “profesionales multidisciplinares” interesados por la hidráulica y la hidrología que también te estarán siguiendo. Continúa profundizando y difundiendo conocimiento. Hacen falta muchos profesionales como tu cuyo objetivo principal no sea el lucro económico.
rauhermi says: 2014/04/02 at 08:08 //
Fernando muchas gracias por tu interés. Tú ya me conoces y sabes que tengo “pasión por el agua”. Yo quiero continuar aprendiendo y difundiendo conocimiento del mundo del agua toda la vida. También hacen falta profesionales como tú cuyo norte sea la honradez y el interés general, a pesar de las dificultades. Un abrazo. Raúl.
Juanjo says: 2014/09/24 at 08:53 //
Hola Rául. Lo primero enhorabuena por el artículo, es muy completo y me ha sido de gran ayuda. Tengo alguna duda con respecto a algunos puntos de la teoría del HUS que te planteo por si puedes echar algo de luz al asunto.
En cuanto al tiempo de desfase a la punta (Tdp), indicas que Tdp = D/0.22; No he encontrado esta expresión en la bibliografía que he encontrado sobre el tema. Si no que la que he encontrado es que:
Tdp = 0.6tc para el HU del SCS.
Tdp = 0.35tc para el Hidrograma Unitario de Témez.
Es decir que dependería de tc (tiempo de concentración). ¿Podrías indicarme de donde viene la expresión Tdp=D/0.22?¿Y por qué no depende de tc? Parece lógico que Tdp dependa de la morfología de la cuenca, que vendría implicita en el tc.
Otra de las dudas que me surgen al analizar el HU es que éstos están definidos para una duración (intervalo de tiempo D) indeterminada. Mi duda es, si hacemos que el tiempo de precipitación de lluvia neta D con intensidad constante, sea igual o mayor al Tconcentración,
teóricamente habrá un momento en el que toda la cuenca esté aportando caudal y este se estabilice (Qpunta). ¿No debería entonces en este caso ser Tp = Tc?
Sin embargo para D = tc
Tp = 0.5D + 0.6tc ; sustituyendo D=tc, Tp = 0.5tc+0.6tc = 1.1tc (Método SCS)
Tp = 0.5D + 0.35tc; sustituyendo D=tc, Tp = 0.5tc+0.35tc = 0.85tc (Método Temez)
Tp = 0.5D+D/0.22; 0.5tc + tc/0.22 = 5.04tc (Según la expresión que propones).
Ninguno de ellos me cuadra con el hidrograma unitario para lluvia con intensidad constante estable durante un tiempo > tc.
Muchas gracias por adelantado, y otra vez enhorabuena por el blog.
Juanjo
rauhermi says: 2014/09/25 at 09:32 //
Buenos días Juanjo, me alegro que te haya resultado útil este artículo. Comentarte que planteas unas inquietudes muy interesantes.
El libro que utilizo normalmente para realizar cálculos hidrológicos es:
“Recomendaciones para el cálculo hidrometeorológico de avenidas” publicado por el Cedex en el año 2.000, y su autor es Javier Ferrer, a quien tuve por profesor en la ETSICCP de Valencia a finales de los noventa y que actualmente es comisario de aguas en la CHJ.
Pienso que en esa publicación puedes resolver todas tus dudas, y si te quedase algo pendiente, lo podemos comentar.
Saludos cordiales desde Murcia. Raúl.
Juanjo says: 2014/09/25 at 10:10 //
Hola Raúl, muchísimas gracias por la información y por tu rápida respuesta. Voy a leerlo con detalle a ver si resuelvo mis dudas. Un saludo.
Juanjo
rauhermi says: 2014/09/27 at 14:38 //
Gracias a ti Juanjo.
Un saludo.
Raúl.
TOAPANTA GABRIEL says: 2018/04/20 at 17:09 //
Buenos días, permitiéndome felicitarlo por la publicación, estoy realizando mi tesis sobre la laminación de crecida de un estanque de retención en un barrio al sur de quito ya esta construido, me podrías ayudar de como realizar el análisis de laminación de crecida, bibliografía, o algún programa que pueda utilizar.
rauhermi says: 2018/04/23 at 07:46 //
Buenos días Gabriel, gracias por tu interés en el blog.
Una opción consiste en utilizar el software HEC-HMS del Hydrologic Engineering Center, del US Army Corps of Engineers. Este software lo puedes descargar en la siguiente dirección http://www.hec.usace.army.mil/software/hec-hms/ y con él podrás incluir elementos de laminación para su análisis.
Un cordial saludo. Raúl.
fernando schujman says: 2018/05/12 at 10:34 //
buenos dias, soy Fernando Schujman , Arquitecto de Tucuman Argentina , Lo felicito por su Blog que aporta claridad sobre las nuevas metodologias de tratamiento hidrico en las ciudades. referido a este tema que en nuestro pais es muy incipiente su conocimiento queria preguntale si es posible utilizar como espacio de laminacion de escorrentias pluviales en la ciudad, los espacios verdes deportivos ,aprovechando su distribucion en el ejido urbano y calificando el uso como mixto, tambien agradeceria me indique si ud conoce alguna bibliografia sobre este topico , o algun trabajo que se refiera al tema, muchas gracias y saludos desde Tucuman
rauhermi says: 2018/05/12 at 17:59 //
Buenas tardes Fernando, gracias por tu interés en el blog.
Para defender un territorio concreto frente a las inundaciones con infraestructura verde es necesario que exista un porcentaje significativo de la superficie en el ámbito de estudio que presente un uso del suelo compatible para ser mantenido sin desarrollo y consolidado como área verde. Además ese espacio verde se debe acondicionar para tal fin (laminación de escorrentías pluviales). Te recomiendo un artículo en el que se describe un ejemplo interesante, se trata de el parque inundable La Marjal situado a poca distancia de la Playa de San Juan en Alicante (España), el enlace es el siguiente https://www.iagua.es/blogs/raul-herrero/desatinos-urbanisticos-infraestructura-verde-defensa-frente-inundaciones
Comparto contigo una carpeta en Dropbox con bibliografía sobre infraestructuras verdes.
Un cordial saludo.
Raúl.
José Hernández says: 2018/06/06 at 19:25 //
Hola Raúl. Se ve que estás en tu elemento: El agua y eres todo un pez!!!. Felicitaciones por tu visión solidaria de compartir conocimientos. Definitivamente estas hecho de material de los dioses. En una época plagada de egoísmo, tu actitud es refrescante y de gran beneficio a los lectores. Ojalá estos no se limiten a recibir, sino también a compartir conocimiento y experiencias.
Te reitero mi admiración y auguro todo lo mejor en tu desempeño profesional.
rauhermi says: 2018/06/07 at 08:38 //
Hola José, gracias por tu interés en el blog y por valorar los conocimientos que se comparten en materia de agua.
Un cordial saludo. Raul.
GABRIEL TOAPANTA says: 2018/07/17 at 00:20 //
buenas noches, excelente informacion, quisiera saber como realizo el Análisis de la laminación para el cálculo del volumen de diseño del depósito de tormentas, de ante mano muchas gracias por la explicacion
rauhermi says: 2018/07/25 at 09:26 //
Hola Gabriel, tal y como te comenté hace unos meses puedes utilizar el software HEC-HMS del Hydrologic Engineering Center, del US Army Corps of Engineers. Este software lo puedes descargar en la siguiente dirección http://www.hec.usace.army.mil/software/hec-hms/ y con él podrás incluir elementos de laminación para realizar el cálculo del volumen del depósito en cuestión.
Otra opción consiste en utilizar una hoja de cálculo, haciendo uso de la metodología de cálculo que se describe en el post que lleva por título “Laminación de embalses” (método de Puls modificado) y que lo puedes encontrar en la siguiente dirección http://eselagua.com/2015/10/30/laminacion-de-embalses/
Un cordial saludo. Raúl.
Felipe Nery Herrera Lemus says: 2022/11/11 at 01:48 //
Excelente aporte